2005——2006学年度第一学期高一期末联考
数学试卷
第I卷(选择题 ,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知A={(x, y)x+y=3}, B={(x,y)x-y=1},则A∩B= ( )
A.{2, 1} B.{x=2,y=1} C.{(2,1)} D.(2,1)
2.若p: x2≥-x, q: x =x , 则p是q的 ( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
3.如果命题“p或q”与命题“非p“都是真命题,则 ( )
A.命题q一定是假命题 B.命题q 一定是真命题
C.命题p一定真命题 D.命题p与命题q真值相同
4.如果函数f(x)的定义域为[-1,1],那么函数f(x2-1)的定义域是 ( )
A.[0,2] B.[-1,1] C.[-2,2] D.[-![]() ,
,![]() ]
]
5.在等比数列{an}中,a1>0且a5·a6=9,则log3a1+log3a2+log3a3+…+log3a10= ( )
A.10 B.12 C.8 D.2+log35
6.已知函数y=f(x)的图象过点A(1,2),函数y=g(x)的图象与y=f(x)的图象关于直线y=x
对称,则y=g(x)的图象必过点 ( )
|
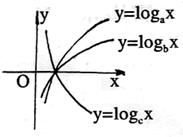
7.由图可推得a、b、c的大小关系是 ( )
A.c<b<a B.c<a<b
C.a<b<c D.a<c<b
8. 若函数y=x2+(2a-1)x+1在区间(-∞,2![]() 上是减函数,则实数a的取值范围是( )
上是减函数,则实数a的取值范围是( )
A.![]() -
-![]() ,+∞) B.(-∞,-
,+∞) B.(-∞,-![]()
![]() C.
C.![]()
![]() ,+∞) D.(-∞,
,+∞) D.(-∞,![]()
![]()
|
10.已知数列{an}的前n项和Sn与第n项an满足Sn=1-nan,则a2= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
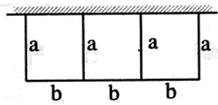
11.一批材料可以建成200m长的围墙,现用这些材料在一边靠墙的地方围成一块矩形场,中间隔成3个面积相等的矩形(如图,则围成的矩形最大总面积为 ( )
|
B.10000m2
C.2500m2
D.6250m2
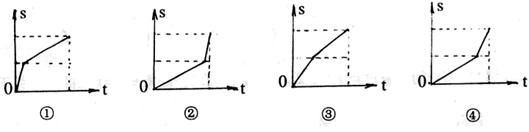
12.甲乙二人同时从A地赶往B地,甲先骑自行车到中点后改为跑步,而乙则是先跑步,到中点后改为骑自行车,最后二人同时到达B地,甲乙两人骑自行车速度都大于各自跑步速度,又知甲骑自行车比乙骑自行车的速度快。若某人离开A地的距离S与所用时间t的函数用图象表示如下,则在下列给出的四个函数中
|
甲乙二人的图象只可能 ( )
A.甲是图①,乙是图② B.甲是图①,乙是图④
C.甲是图③,乙是图② D.甲是图③,乙是图④
第II卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分。请将答案写在题中的横线上)
13.在数列{an}中,an=-4n+15,则前n项和的最大值为 .
14.函数![]() 的定义域为
.
的定义域为
.
15.若f(x-1)=x-x-2,则f(log23)= .
16.对于下列条件
①数列{ an}的通项公式an是关于n的一次函数
②数列{ an}的前n项和Sn=an2+bn(a、b为常数)
③数列{ an}对任意n∈N*均有a2n-a2n-1=d(d为常数)
④数列{ an}对任意n∈N*均有an+an+2=2an+1
可作为使{ an}成等差数列的充要条件的是 (把你认为正确的条件序号都填上)
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程及演算步骤。)
17.(本小题满分10分)
已知集合A={x![]() ≤0}, B={xx2-3x+2<0}, U=R,
≤0}, B={xx2-3x+2<0}, U=R,
求(Ⅰ)A∩B;
(Ⅱ)A∪B;
(Ⅲ)(![]() uA)∩B.
uA)∩B.
18.(本小题满分12分)
判断二次函数f(x)=ax2+bx+c(a<0)在区间![]() 上的增减性并依定义给出证明。
上的增减性并依定义给出证明。
19.(本小题满分12分)
已知函数f(x)=![]() 的定义域为(-∞,2
的定义域为(-∞,2![]()
(I)求函数f(x)的值域;
(Ⅱ)求函数f(x)的反函数f-1(x).
20.(本小题满分12分)
已知函数![]() (a、b是常数且a>0,a≠1)在区间[-
(a、b是常数且a>0,a≠1)在区间[-![]() ,0]上有ymax=3,
,0]上有ymax=3,
ymin=![]() ,试求a和b的值.
,试求a和b的值.
21.(本小题满分14分)
在等比数列{an}中,前n项和为Sn,若S2,S4,S3成等差数列,则a2, a4, a3成等差数列.
(Ⅰ)写出这个命题的逆命题;
(Ⅱ)判断逆命题是否为真,并给出证明.
22.(本小题满分14分)
某公司实行股份制,一投资人年初入股a万元,年利率为 25%,由于某种需要,从第二年起此投资人每年年初要从公司取出x万元.
(Ⅰ)分别写出第一年年底,第二年年底,第三年年底此投资人在该公司中的资产本利和;
(Ⅱ)写出第n年年底此投资人的本利之和bn与n的关系式(不必证明);
(Ⅲ)为实现第20年年底此投资人的本利和对于原始投资a万元恰好翻两番的目标,若a=395,则x的值应为多少?(在计算中可使用lg2=0.3)
数学试题参考答案及评分标准
一、C A B D ; A A B B ; C B C B
二、13.21; 14.{x-2≤x<-1}; 15.2; 16.②,④
三、(17)
解:A={x![]() ≤0}={x-5<x≤
≤0}={x-5<x≤![]() }……………………2分
}……………………2分
B={xx2-3x+2<0}={x1<x<2}…………………………4分
(Ⅰ)A∩B={x1<x≤![]() }…………………………………6分
}…………………………………6分
(Ⅱ)A∪B={x-5<x<2}………………………………8分
(Ⅲ)(![]() uA)={xx≤-5或x>
uA)={xx≤-5或x>![]() } (
} (![]() uA)∩B={x
uA)∩B={x![]() <x<2}…………10分
<x<2}…………10分
18.解:f(x)在![]() 上是减函数……………………………………………………1分
上是减函数……………………………………………………1分
设x1,x2∈![]() 且x1<x2…………………………………………………………2分
且x1<x2…………………………………………………………2分
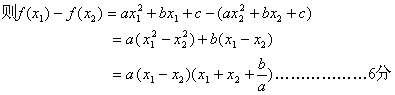
∵x1 , x2 ∈![]() ∴-
∴-![]() < x1 +x2<+∞…………………………………………8分
< x1 +x2<+∞…………………………………………8分
∴x1 +x2+ ![]() >0,而x1 -x2<0, a<0……………………………………………………10分
>0,而x1 -x2<0, a<0……………………………………………………10分
∴f(x1)-f(x2)>0 即f(x1)>f(x2)
∴二次函数f(x)=ax2+bx+c(a<0)在区间![]() 上是减函数………………………12分
上是减函数………………………12分
19.解:(I)∵x≤2 ∴0<2x≤4 …………………………………………………………2分
∴4≤8-2x<8 ∴![]() 8<
8<![]() ≤
≤![]() 4…………………………………4分
4…………………………………4分
即-3<![]() ≤-2 ∴-3<y≤-2
≤-2 ∴-3<y≤-2
∴函数y=![]() 的值域为(-3,-2
的值域为(-3,-2![]() ………………………………7分
………………………………7分
(Ⅱ)由y=![]() 得
得![]() =8-2x……………………………………9分
=8-2x……………………………………9分
∴2x=8-![]() ∴x=log2(8-2-y)
∴x=log2(8-2-y)
∴f-1(x)=log2(8-2-x)(-3<x≤-2)…………………………………………12分
20.解:令u=x2+2x=(x+1)2-1 x∈[-![]() ,0]
,0]
∴当x=-1时,umin=-1 当x=0时,umax=0…………………………3分
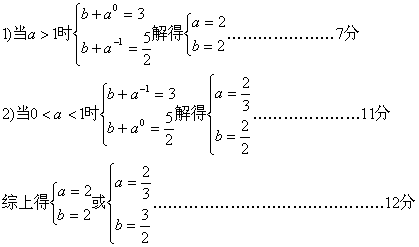
21.解(I)逆命题:在等比数列{an}中,前n项和为Sn,若a2 , a4, a3成等差数列,则S2,S4,S3成等差数列………………………………3分
(II)设{an}的首项为a1,公比为q
由已知得2a4= a2 + a3 ∴2a1q3=a1q+a1q2
∵a1≠0 q≠0 ∴2q2-q-1=0 ∴q=1或q=-![]() ……………………5分
……………………5分
当q=1时,S2=2a1, S4=4 a1,S3=3 a1,
∴S2+S3≠2 S4 ∴S2,S4,S3不成等差数列………………………………9分
当q=-![]() 时
时
S2+S3=(a1+a2)+( a1+a2+a3)=2[a1a1×(-![]() )]+a1(-
)]+a1(-![]() )2=
)2=![]() a1
a1
2 S4=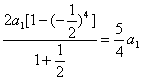
∴S2+S3=2 S4 ∴S2,S4,S3成等差数列………………………………13分
综上得:当公比q=1时,逆命题为假
当公比q≠1时,逆命题为真……………………………………14分
22.解:(I)第一年年底本利和:a+a·25%=1.25a…………………………1分
第二年年底本利和:(1.25a-x)+(1.25a-x)25%=1.252a-1.25x…………3分
第三年年底本利和:(1.252a-1.25x-x)+(1.252a-1.25x-x)25%
=1.253a-(1.252a+1.25)x…………………………5分
(II)第n年年底本利和:bn=1.25na-(1.25n-1+1.25n-2+…+1.25)x…………………8分
(III)依题意有:
395×1.2520-(1.2519+1.2518+…1.25)x=4×395…………………………………………10分
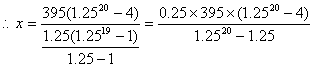 ①………………………12分
①………………………12分
设1.2520=t ∴lgt=201g(![]() )=20(1-31g2)=2
)=20(1-31g2)=2
∴t=100代入①解得x=96………………………………………………14分