高一数学必修Ⅱ第一章与第二章期末练习题

一、选择题

1、下列说法中正确的是(　 )

A、三点确定一个平面　　　　　 B、空间四点中如果有三点共线，则这四点共面

C、三条直线两两相交，则这三条直线共面　　　　　 D、两条直线确定一个平面

2、下列命题中，正确的是（　　 ）

A、有两个面互相平行，其余各面都是等腰梯形所围成的几何体叫做棱台；

B、有一个面是多边形，其余各面都是三角形所围成的几何体是棱锥；

C、三棱锥的侧面或底面不可能是直角三角形；

D、三棱锥又叫四面体。

3、梯形（如图）是一水平放置的平面图形的直观图（斜二测），

若∥轴，∥轴，，

，则平面图形的面积是（　　　）

A、5　　　　　 B、10　　　　 C、　　　　 D、

4、两条异面直线在同一平面的正投影不可能是（　 ）

A、两条平行直线　　 B、两条相交直线　　 C、一个点和一条直线　　　D、两个点

5、在棱长为1的正方体中，由在表面到达的最短行程为（　　）

　A、　　　　  B、　　　　  C、　　　　　　 D、3

6、正六棱台的两底面的边长分别为和2，高为，则它的体积为（　　）

  A、　　　 B、　　　　 C、　　　　 D、

7、已知直线⊥平面α，直线m平面β，有下面四个命题：

①；②；③；④，

其中正确的两个命题的序号是

A、①与②　　　　　　B、③与④ 　　　　　　　　 C、②与④　　　　　　　 D、①与③

8、直线⊥平面,直线‖平面,则 与的关系为(　 )

A、⊥且与相交　　　 B、⊥且与不相交

C、　　　　　　　　　 D、与一定不垂直

9、如图是正三棱锥（底面边为4，高为4），则它的三视图是（　　）

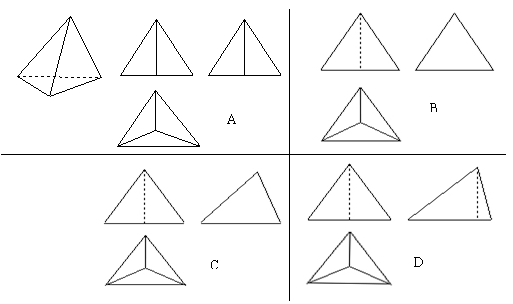10、给出下列四个命题：

（1）垂直于同一条直线的两条直线平行；（2）垂直于同一条直线的两个平面平行；

（3）垂直于同一平面的两条直线平行； （4）垂直于同一平面的两平面平行。

其中正确命题的个数为

A、1　　　　 B、2　　　　　  C、3　　　　  D、4

11、已知圆锥的表面积是底面积的3倍，那么该圆锥的侧面展开图扇形的圆心角为（　　）

　A、120⁰ B、150⁰　　　　  C、180⁰　　　　D、240⁰

12、能保证直线与平面平行的条件是（　　  ）

　A、∥　　　　　　  B、∥

　C、∥，∥，∥　　 D、∥

二、填空题

13、已知球的一个截面的面积为，且此截面到球心的距离为4，则该球的表面积为_________。

14、　　 14、三棱锥三条侧棱两两互相垂直，三个侧面积分别为1.5cm²、2cm²、6cm²，则它的体积为　　　　　  。

15、空间四边形中，、分别是、的中点，=3、= 4、=,那么与所成角的度数是_________。

16、已知点P是△ABC所在平面外一点，点O是点P在平面上的射影，若点P到△ABC 的三个顶点的距离相等，则O是△ABC 的______，若△ABC是直角三角形，则O位于　　　　 。

三、解答题

17、 已知底面半径为的圆锥，它的全面积为，当为何值时，圆锥的体积最大？最大体积是多少？

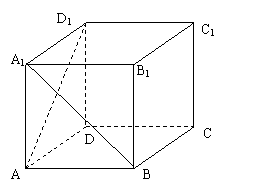18、已知正方体，求：

（1）异面直线与所成的角；

（2）求与平面所成的角；

（3）二面角的大小；

19、试构造出一个三棱锥S—ABC，使其四个面中成直角三角形的个数最多，作出图形，

指出所有的直角，并证明你的结论。

20、在三棱锥中,、分别为△ABC和△BCD的重心。

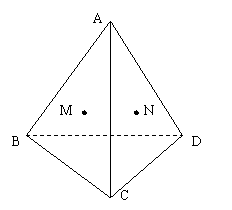求证:∥

　　　　　　　　　　　　　　　　　　　　

21、如图,已知四棱锥的侧面是正三角形, 是的中点

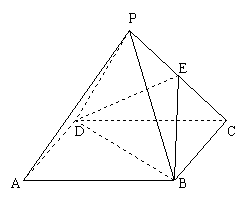　　求证:（1）∥平面；

　　　　 （2）平面平面。

22、直角三角形三边长分别是3cm、4cm、5cm，绕三边旋转一周分别形成三个几何体。想象并说出在个几何体的结构，画出它们的三视图，求出它们的表面积和体积。