池州市2004—2005学年度第一学期期末教学质量检测

高一数学试题

(满分120分　 时间120分钟)

题号	一	二	三	总分
得分

一、选择题（12×4’=48’）

1、函数y=f（x）的图象与直线x=a的交点个数是[　　 ]。

A、0　　 B、1　　 C、至多1个　　 D、至少1个

2、集合P={xy=　  　} ，集合Q={yy=　　 }，则P与Q的关系是[　　]。

A、P=Q　　B、P　 Q　　C、P　 Q　 D、P ∩Q=φ

3、定义A—B={xx∈A且xB}，若M= {1、2、3、4、5}，N={2、3、6}，则N—M=[　　 ]。

A、M　　 B、N　　 C、{1、4、5}　　D、{6}

4、关于x的不等式x—a ＞b（b<0）的解集是[　　　]。

A、{xx∈R且x≠a}　 B、R　　C、{ xx＜b}　 D、φ

5、若命题P和Q满足“若P则Q”为真，那么“非P”是“非Q”是[　　 ]。

A、充要条件　 　　　B、充分条件　 　

C、必要条件　　　　 D、不充分也不必要条件

6、若函数y=f（x）的图象经过点（0，1），则y=f（x+4）的反函数的图象必经过[　  ]。

A、（4，1）　 B（-4，1）　 C、（1，4）  D、（1，-4）

7、设a=　　 　　　　　　　 ， 则a∈[　　　]。

A、（0，1）　B、（1，2）　 C、（2、3）  D、（3，4）

8、在数列1，1，2，3，5，8，13，x，34，55，……中，x=[　 ]。

A、19　　 B、20　　 C、21　　 D、22

9、在等差数列{a_n}中，S_n表示该数列前n项之和，S₁₀=100，S₂₀=400，则S₃₀=[　　]。

A、500　　B、300　　 C、900　　 D、700

10、某企业生产总值的月平均增长率为P，则年平均增长率为[　 ]。

A、（1+P）¹¹　　 B、（1+P）¹² 　　C、（1+P）¹²—1　　D、（1+P）¹¹—1

11、如果数列{ a_n }满足a₁，a₂—a₁，a₃—a₂，……，a_n—a_n-1，……是首项为1，公比为2的等比数列，那么a_n=[　　]。

A、2ⁿ⁺¹—1 　　B、2ⁿ—1 　　C、 2^n-1 　　　D、2ⁿ + 1

12、一个首项为正数的等差数列{ a_n }，已知S₅= S₁₃，那么这个数列的前[　　]项之和最大。

A、S₈　　　B、S₁₀　　 C、S₇　　 D、S₉

二、填空题（4×4’=16’）

13、已知lg3 = 0.4771，lgx = —1.5229，则x =　　　　 ；

14、已知函数f（x）=a^x（a＞0且a1≠1）在[1，2]上的最大值比最小值大a /2 ，则a=　　　　 ；

15、数列{a_n}满足a₁=2，a_n+1= —　　　　，则a₂₀₀₅ = 　　　　　　；

16、设f（x）是定义在R上的函数，对任意实数x,y都有

f（xy+1）=f（x）·f（y）—f（y）—x+2且，f（0）=1，则f（x）=　　　　。

三、解答题

17、设集合A={x—2x²—7x+15＞0}，B={x x² + ax + b≤0}，若A∩B=ф且

A∪B={x—5＜x≤2 }，求实数a，b的值。 （7分）

18、化简:　 　　　　　　　　　　　　　　　　　　　　 (7分)

19、已知数列{a_n}的前n项和S_n= 10n—n²，设T_n = a₁ + a₂+…+ a_n，求T_n (8分)。

20、已知等比数列{a_n}的公比为q，前n项之和为S_n，且S₃，S₉，S₆，成等差数列。

（1）求q³的值,

（2）求证：a₂，a₈，a₅成等差数列 （8分）。

21、已知函数f（x）=2^x—1的反函数f^{- -1}（x），g（x）=log₄（3x+1）

（1）若f^{- -1}（x）≤g（x）求x的取值集合D ，

（2）设函数H（x）= g（x）—0.5f ^-1（x），当x∈D时，求函数H（x）的值域。(12分)

22、已知函数f（x）=（x—1）² ，g（x）=4（x—1），数列{a_n}满足a₁=2，a_n≠1，

（a_n+1—a_n）g（a_n）+ f（a_n）=0

（1）求证：a_n+1=　　　a_n +　　，

（2）求数列{a_n—1}的通项公式，

（3）若b_n=3 f（a_n）—g（a_n+1），求{b_n}的最大项和最小值。（14分）

池州市2004—2005学年度第一学期期末教学质量检测

高一数学答案

一、选择题

1（C）　 2（C）　 3（C）　 4（B）　 5（C）　 6（D）

7（C）　 8（C）　 9（C）　 10（C） 11（B）　12（D）

二、填空题

13、　　　　　 14、　　　　　15、2　　　　　　16、x+1

三、解答题

17、解：由-2x²-7x+15>0得A=（-5，）（2分）

　　　  ∵A∩B=，且A∪B={x-5<x≤2}　则

B=[，2]（4分）

∴方程x²+ax+b=0的两根为，2，由韦达定理知

-a=+2

　　　  （6分）　　 得a=，b=3（7分）

b=×2

18、解：原式=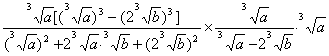（5分）

　　　　　  =　　（6分）

　　　　　  =a　　　　　　 （7分）

19、解：∵S_n=10n-n²，当n=1时a₁=9（1分）

当n≥2时a_n=S_n-S_n-1=11-2n（2分）

∴a_n=11-2n(n∈N)（3分）

∵当1≤n≤5时，a_n>0，而当n≥6时a_n<0

1、当1≤n≤5时，T_n=a₁+a₂+…+a_n=10n-n²（5分）

2、当n≥6时，T_n=a₁+a₂+…+a₅-a₆-a₇…-a_n

　　　　　　 =2S₆-S_n=n²-10n+50（7分）

　　　  10n-n²（1≤n≤5）

∴Tn=　 　　　　　　　　　　　　（8分）

n²-10n+50（n≥6）

20、解：（1）设{a_n}的前项为a₁，公比为q，由S₃、S₉、S₆成等差数列，得S₃+S₆=2S₉，若q=1，则S₃+S₆=9a₁，2S₉=18a₁

∵a₁≠0　　 ∴S₃+S₆≠2S₉，从而q≠1，（2分）

由S₃+S₆=2S₉得

整理得q³+q⁶=2q⁹（3分）

由q≠0、1，得q³=（4分）

（2）由（1）知：a₈=a₂×q⁶=a₂，a₅= a₂×q³=a₂（6分）

　∴a₈-a₂=a₅-a₈所以a₂、a₈、a₅成等差数列　 （8分）

21、解（I）因为f(x)=2^x-1　 ∴f^-1(x)=log₂(x+1)(x>-1)（2分）

　　　由f^-1(x) ≤g(x)得log₂(x+1) ≤log₄(3x+1)

 ∴　x+1>0

 (x+1)²≤3x+1（4分）解得0≤x≤1，即D=[0,1]（6分）

（II）H(x)=log₄(3x+1)-log₂(x+1)=（8分）

　　 由0≤x≤1得1≤3-≤2（10分）

∴0≤≤（11分）s

∴H(x)在D上的值域为[0、]（12分）

22、解（1）∵(a_n+1-a_n)g(a_n)+f(a_n)=0（1分）

又g(a_n)=4(a_n-1)，f(a_n)=(a_n-1)²（2分）

∴(a_n-1)(4a_n+1-3a_n-1)=0（3分）

而a_n≠1

∴a_n+1=a_n+（4分）

（2）由（1）知a_n+1-1=(a_n-1)，而a₁-1=1（6分）

∴{a_n-1}是首项为1，公比为的等比数列（7分）

∵a_n-1=()^n-1（8分）

（3）由（2）知，a_n=()^n-1+1则b_n=

即b_n=3[()^n-1-]^2s-（n∈N）（9分）

令()^n-1=()^x=u（x∈N）且y=b_n

则y=3(u-)²-（0<u≤1）（10分）

∵当u∈(0，]时，y是u的减函数；

当u∈[，1]时，y是u的增函数

∴u=1即n=1时，y有最大值

∴{b_n}中最大项b₁=0（12分）

又∵当n=2时，()^2-1-=；

　　当n=3时，()^3-1-=；

　　当n=4时，()^4-1-=；而>=

∴n=3时，即{b_n}中b₃最小，b₃=（14分）