成都市2004~2005学年度上期期末调研考试
高一数学
本试卷分为A、B卷。A卷100分;B卷50分,全卷总分150分,考试时间120分钟。
A 卷(共100分)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的。(每小题5分,共50分)
1.集合{0,1,2}的所有真子集的个数是( )
A.5 B.6
C.7 D.8
2.若集合M={(x,y)x+y=0},P={(x,y)x-y=2},则M![]() P是( )
P是( )
A.(1,-1) B.{x=1}![]() {y=-1}
{y=-1}
C.{1,-1} D.{(1,-1)}
3.设M=R,从M到P的映射![]() ,则象集P为( )
,则象集P为( )
A.{yy![]() R} B.{yy
R} B.{yy![]() R+}
R+}
C.{y0≤y≤2} D.{y0<y≤1}
4.条件p∶x=x,条件q∶x2≥-x,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知数y=x2+2(a-2)x+5在区间(4,+![]() )上是增函数,则实数a的取值范围是( )
)上是增函数,则实数a的取值范围是( )
A.a≤-2 B.a≥-2
C.a≤-6 D.a≥-6
6.三个数成等差数列,其平方和为450,两两之积的和为423,则中间一个数为( )
A.±12 B.![]()
C.![]() D.150
D.150
7.如果数列{an}的前n项和Sn=![]() an-3,那么这个数列的通项公式是( )
an-3,那么这个数列的通项公式是( )
A.an=2(n2+n+1) B.an=3·2n
C.an=3n+1 D.an=2·3n
8.已知等差数列{an}的公差是2,且a1+a2+a3+…+a100=100,那么a4+a8+a12+…+a100=( )
A.25 B.50
C.75 D.100
9.函数y=log2x的大致图象是( )

![]()
![]()
二、填空题:把答案直接填在题后的横线上。(每小题5分,共20分)
11.命题“若ab=0,则a=0或b=0”的逆否命题是_____,它是_____命题(填“真”或“假”)。
12.![]()
13.已知集合M={xax2+2x+1=0}只含有一个元素,则a=_______。
14.在等比数列{an}中,a1+a2+a3=-3,a1·a2·a3=8,则an=_______。
三、解答题:解答应写出文字说明,说明过程或演算步骤。(共30分)
15.(共9分)将长为a的铁丝折成矩形,将矩形面积y表示为矩形一边长x的函数,求此函数的定义域和值域。
16.(共10分)讨论函数y=lg(x2-2x-3)的单调性。

B 卷(共50分)
四、填空题:(每小题4分,共16分)
18.![]()
19.![]()
20.![]()
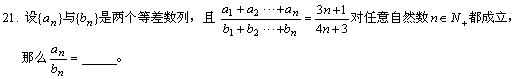
五、解答题:(共34分)解答写出文字说明、证明过程或演算步骤。
22.(共10分)若0<x<1,a>0,a≠1,试比较p=loga(1-x)和q=loga(1+x)的大小。
23.(共12分)某种商品的价格为每件a元,若涨价x成时,卖出的数量便减少mx成(m为正常数)。
(Ⅰ)当m=0.8时,应涨几成价格,才能使售出的商品总金额最大?
(Ⅱ)若适当地涨价,能使销售款增加,那么m的值在什么范围内?
24.(共12分)已知数列{an}的前n项和Sn=pn+q(p≠0,p≠1),求数列{an}是等比数列的充要条件。
成都市2004~2005学年度上期期末调研考试
高一数学参考答案及评分标准
A 卷
一、选择题:(每小题5分,共50分)
1.C 2.D 3.D 4.A 5.B 6.A 7.D 8.D 9.C 10.C.
二、填空题:(每小题5分,共20分)
11.若a≠0且b≠0,则ab≠0,真命题.
12.y=(![]() )x+1(x<-1).
)x+1(x<-1).
13.a=0或a=1;
14.an=-(-2)n-1或an=-4(-![]() )n-1.
)n-1.
[注:13、14题写正确一个者,也相应给分]
三、解答题:(共30分)
15.解:由题意,有
y=x(![]() -x).
……(3分)
-x).
……(3分)
从而y=x(![]() -x)=-(x-
-x)=-(x-![]() )2+
)2+![]() .
……(2分)
.
……(2分)
故函数y=x(![]() -x)的定义域为(0,
-x)的定义域为(0,![]() ),值域为(0,
),值域为(0,![]() ]. ……(4分)
]. ……(4分)
16.解:令u=x2-2x-3,则u=(x-1)2-4,y=lgu. ……(2分)
∵x2-2x-3>0,∴(x-3)(x+1)>0,∴x>3或x<-1. ……(3分)
当x∈(-∞,-1)时,若x增,则u减,此时y减; ……(2分)
当x∈(3,+∞)时,若x增,则u增,此时y增; ……(2分)
∴函数y=lg(x2-2x-3)在(-∞,-1)上随x增大而减小,在(3,+∞)上随x的增大而增大. ……(1分)
17.解:设d为{an}的公差.
∵![]() =(
=(![]() =(
=(![]() )d为常数, ……(2分)
)d为常数, ……(2分)
∴数列{bn}是等比数列,设其公比为q.
∵b1·b2·b3=![]() ,∴
,∴![]() ·b2·b2q=
·b2·b2q=![]() ,
,
∴b2=![]() .
……(2分)
.
……(2分)
∵b1+b2+b3=![]() ,∴
,∴![]() +
+![]() +
+![]() =
=![]() ,
,
∴q=![]() 或4.
……(2分)
或4.
……(2分)
当q=![]() 时,bn=b1·qn-1=b2qn-2=
时,bn=b1·qn-1=b2qn-2=![]() ·(
·(![]() )n-2=(
)n-2=(![]() )2n-3,从而an=2n-3;……(2分)
)2n-3,从而an=2n-3;……(2分)
当q=4时,bn=b2·qn-2=![]() ·4n-2=(
·4n-2=(![]() )-2n+5,从而an=-2n+5.
……(2分)
)-2n+5,从而an=-2n+5.
……(2分)
∴an=2n-3或an=-2n+5. ……(1分)
B 卷
四、填空题:(每小题4分,共16分)
18.(-∞,-2);
19.f(x)=x2-1(x≥1).(注:无定义域者不得分)
20.(-∞,-3].
21.![]() =
=![]() .
.
五、解答题:(共34分)
22.解:∵0<x<1,∴1-x∈(0,1),1+x∈(1,2),1-x2∈(0,1). ……(3分)
①若a>1,则loga(1-x)<0,loga(1+x)>0,∴q-p=loga(1+x)+loga(1-x)=
loga(1-x2)<0. ∴p>q. ……(3分)
②若0<a<1,则loga(1+x)<0,loga(1-x)>0,∴ q-p=-loga(1+x)+loga(1-x)=- loga(1-x2)<0. ∴p>q. ……(3分)
故恒有p>q. ……(1分)
23.解:(Ⅰ)设卖出b件商品,则售出货款为y=ab. ……(1分)
若涨价x成,每件售价为a(1+![]() )元,卖出了b(1-
)元,卖出了b(1-![]() )件,售出总金额为
)件,售出总金额为
y=ab(1+![]() )(1-
)(1-![]() ).
……(2分)
).
……(2分)
当m=0.8时,y=ab(1+![]() )(1-
)(1-![]() x)=ab[-
x)=ab[-![]() (x-
(x-![]() )2+
)2+![]() ]. ……(2分)
]. ……(2分)
故当x=![]() 时,y取最大值,即涨价125%时,售出的总金额最大. ……(2分)
时,y取最大值,即涨价125%时,售出的总金额最大. ……(2分)
(Ⅱ)y=ab(1+![]() )(1-
)(1-![]() )=
)=![]() {-[x-
{-[x-![]() ]2+
]2+![]() +
+![]() }.……(2分)
}.……(2分)
当x=![]() 时,y取最大值;当x=0时,售货款没有增加,为使涨价后售货款增多,应有
时,y取最大值;当x=0时,售货款没有增加,为使涨价后售货款增多,应有![]() >0,
……(2分)
>0,
……(2分)
解得0<m<1. ……(1分)
24.解:由a1=S1=p+q. ……(1分)
当n≥2时,an=Sn-Sn-1=pn-1(p-1). ……(2分)
∵p≠0,p≠1,
∴![]() =
=![]() =p.
……(2分)
=p.
……(2分)
必要性:若{an}是等比数列,则
![]() =
=![]() =p,
=p,
∴![]() =p.
=p.
∵p≠0,∴p-1=p+q,∴q=-1. ……(3分)
充分性:当q=-1时,a1=p-1,满足an=pn-1(p-1),
∴an=pn-1(p-1)(n∈N+).
∴![]() =p(n∈N+)
=p(n∈N+)
∴{an}是等比数列. ……(3分)
∴q=-1是数列{an}为等比数列的充要条件. ……(1分)