第三章 概率 练习题

一．选择题  （ 每题 4分　 共 40分 ）

1．下列结论正确的是（ C　 ）

A. 事件A的概率P(A)必有0<P(A)<1

B. 事件A的概率P(A)=0.999,则事件A是必然事件

C. 用某种药物对患有胃溃疡的500名病人治疗，结果有380人有明显的疗效 ，现有胃溃疡的病人服用此药，则估计其明显疗效可能性为76％。

D. 某奖券中奖率为50％，则某人购买此券10张，一定有5张中奖。

2．下列说法正确的是（D　 ）

A. 事件A、B至少有一个发生的概率一定比A、B中恰有一个发生的概率大

B. 事件A、B同时发生的概率一定比事件A、B恰有一个发生的概率小

C. 互斥事件一定是对立事件，对立事件不一定是互斥事件

D.互斥事件不一定是对立事件，对立事件一定是互斥事件

3 。抽查10件产品。设事件A：至少两件次品，则  　为（　B）

A．至多两件次品　　　　　 B　至多一件次品

C. 至多两件正品　　　　　 D　至少两件次品

4．用1、2、3、4、5做成无重复数字的五位数，这些数被2整除的概率是（　C ）

A　　　 B　　　　 C　 　　 D　

5．一批零件有10个，其中有8个合格品，2个次品，每次任取一个零件装配机器，若第一次取到合格品的概率为 P₁ ,第二次才取到合格品的概率为P₂ 则（　A ）

A. P₁>P₂B　P₁=P₂　　 C　P₁<P₂ D　P₁=2P₂

6. 现有5根细木棒，长度分别为1、3、5、6、9 (cm) ,从中任取三根，能搭成三角形的概率是（ C　）

A . 　　　 B 　　　　C　　　　D　

7. 有100件产品，其中有5件不合格品，从中有放回地连续抽两次，则第一次抽到不合格品，第二次抽到合格品的概率为（C  ）

A　　　　B　　　　C　　　　　 D　　

8 . 从整数中任取两数，其中是对立事件的是  （ C ）

① 恰有一个是偶数和恰有一个是奇数

②至少有一个是奇数和两个都是奇数

③ 至少有一个是奇数和两个都是偶数

④ 至少有一个奇数和至少有一个偶数

A .①　　　　 B ②④　　　  C　③　　　 D　①③

9. 打靶时，甲每打10次可中靶8次，乙每打10次可中靶7次，若两人同时射一个目标，则甲乙两人至少有一人中靶的概率是（ A）

A　0.94　　 B　0.93　　C　0.92　　　 D　0.95

10.　在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于的概率是（C  ）

A.  　　 B　　　　C　 　　 D　

二 填空题　（每题5分　　共　 5分×4＝20分　 ）

11　抛掷一个骰子的一次试验，事件A表示奇数点向上，事件B表示向上的点数不超过3，则P(A+B)=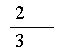

12  袋中有5个白球，3个黑球，从中任取3个球，则至少有一个白球的概率是　

13　从甲、乙、丙、丁四人中选两名代表，甲被选中的概率是　

14　在区间（0，L）内任取两点，则两点间的距离小于的概率

三　解答题

15．某人进行射击表演，已知击中10环的概率为0.35，击中9环的概率为0.30，击中8环的概率为0.25，现在他射击一次，问击中8环以下（不含8环）的概率是多少？

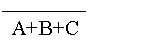解：记=“击中10环”　，B=“击中9环” ，C=“击中8环” ，D=“击中8环以下”　  则：D=　　　　　 ,且A、B、C互斥，

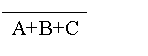所以 P(D) =P(　　　　　 )

　　　　  =1-P(A+B+C) =1-[P(A)+P(B)+P(C)]

　　　　　　  = 1-[0.35+0.30+0.25]=0.1

 

 16．在一次口试中，要从5道题中随机抽出3道题进行回答，答对其中的2道题就获得优秀，答对其中的1道就获得及格，某考生会回答5道题中的2道题，试求：

（1） 他获得优秀的概率是多少？

（2） 他获得及格与及格以上的概率是多大？

解：从5道题中任取3道回答，共有（1，2，3），（1，2，4），（1，2，5）

（1，3，4），（1，3，5），（1，4，5），（2，3，4），（2，4，5），（3，4，5）

10个基本事件。

（1）设A＝{ 获得优秀}，则随机事件A包含 基本事件个数m=3种

；故事件A的概率为P(A)=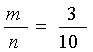

（2）设B＝{获得及格与及格以上}，则事件B所包含的基本事件个数

m=9种，故事件B的概率P(B)=

答：这个考生获得优秀的概率为 ，获得及格与及格以上的概率为 。17．从1，2，3，4，5五个数字中，任意有放回地连续抽取三个数字，求下列事件的概率：

　 （1）三个数字完全不同；

　 （2）三个数字中不含1和5 ；

　 （3）三个数字中5恰好出现两次

解：从五个数字中，任意有放回地连续抽取三个数字，相当于完成这件事分三步，每步从5个元素中均取出一个元素，有5种不同的方法，因此共有5×5×5＝125种不同的结果。

（1）三个数字完全不同相当于第一步有5种方法，第二步有4种方法，第三步有3种方法，故有5×4×3＝60种，所以三个数字完全不同的概率为

P₁= .

(2) 三个数字中不含1和5，相当于每次只能从其他三个数字中有放回地抽取出一个数字，故共有3³＝27种，因此概率P₂=

(3)先研究第一次5，第二次5，第三次非5的方法数，相当于第一次取5，第二次取5，第三次取非5，共有1×1×4＝4种不同的方法，所以恰有两次取5的方法数为12种，所以三个数字种5恰好出现两次的概率为P₃=

18．平面上画了一些彼此相距2a　　 的平行线，把一枚半径r<a的硬币任意掷在平面上，求硬币不与任一条平行线相碰的概率

解：设事件A：“硬币不与任一条平行线相碰”，为了确定硬币的位置，由硬币中心O向靠得最近的平行线引垂线OM，垂足为M,如上图所示，这样线段OM的长度(记作│OM│)的取值范围是[0,a] ,其长度就是几何概型定义中区域Ω的几何度量，只有当r<│OM│≤a时硬币不与平行线相碰，其长度就是子区域A的几何度量，所以

P(A)=

19．十七世纪意大利的赌徒们认为：两颗骰子掷出的点数和为5和与掷出的点数和为9的概率是相等的，你认为他们的看法对吗？为什么？

解：抛两颗骰子的结果总数为6×6＝36

　　设A=“点数之和为5”,则A包含的基本事件的个数为4个，其概率为P(A)=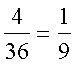

设B=“点数之和为9”，则事件B包含的基本事件的个数为4个，其概率为P(B)=

所以  P(A)=P(B)　 即他们的说法是正确的。