泰州市2005~2006学年度第一学期期末联考
高一数学试题
(考试时间:120分钟 总分150分)
注意事项:
1、本试卷共分两部分,第Ⅰ卷为选择题,第Ⅱ卷为填空题和解答题。
2、所有试题的答案均填写在答题纸上(选择题部分使用答题卡的学校请将选择题的答案直接填涂到答题卡上),答案写在试卷上的无效。
公式:棱锥的体积V=![]() sh; 球的表面积S=4πR2
sh; 球的表面积S=4πR2
第I卷(选择题 共60分)
一、选择题:(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项符合题意要求.)
1.设集合P={1,2,3,4},Q={x x≤2,x![]() R},则P
R},则P![]() Q等于
Q等于
A.{1,2} B.{3,4} C.{1} D.{-2,-1,0,1,2}
2.下列三个数:![]() 的大小顺序是
的大小顺序是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下图是某物体的直观图,在右边四个图中是其俯视图的是
![]()

A. B. C. D.
4.己知函数y=x2的值域是[1,4],则其定义域不可能是
A.[1,2]
B.[-![]() ,2]
,2]
C.[-2,-1] D.[-2,-1)∪{1}
5.下列判断正确的是
A.定义在R上的函数f(x),若f(-1)=f(1),且f(-2)=f(2),则f(x)是偶函数
B.定义在R上的函数f(x)满足f(2)>f(1),则f(x)在R上不是减函数
C.定义在R上的函数f(x)在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上也是减函数,
上也是减函数,
则f(x)在R上是减函数
D.既是奇函数又是偶函数的函数有且只有一个
6.圆x2+y2-2ax+3by=0(a>0,b>0)的圆心位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.圆x2+y2-2x-3=0与直线y=ax+1交点的个数为
A.0个 B.1个 C.2个 D.随a值变化而变化
8.一组实验数据如下表
| t | 1.02 | 1.99 | 3.01 | 4.00 | 5.10 | 6.12 |
| V | 0.01 | 1.50 | 4.40 | 7.50 | 12.09 | 18.01 |
与两个变量之间的关系最接近的是下列关系式中的
A.V=log2t B.V=-log2t C. V=2t-2 D. V=(t2-1)
 9.如图正方形O’A’B’C’的边长为1cm,它是水平放置的一个平面图形的直观图,则原
9.如图正方形O’A’B’C’的边长为1cm,它是水平放置的一个平面图形的直观图,则原
图形的周长是
A.8cm B.6 cm
C.2(1+![]() )cm D.2(1+
)cm D.2(1+![]() )c m
)c m
10.设P、A、B、C是球O表面上的四个点,PA、PB、PC两两
互相垂直,且PA=3,PB=4,PC=5,则球的表面积为
A.![]() π B.25π
C. 50π
D. 100π
π B.25π
C. 50π
D. 100π
11. 下面三条直线l1:4x+y=4,l2:mx+y=0,l3:2x-3my=4不能构成三角形,则m的集合是
A.{-1,![]() } B.{4,
} B.{4,![]() } C.{-1,
} C.{-1,![]() ,
,![]() ,4} D.{-1,
,4} D.{-1,![]() ,0,
,0,![]() ,4}
,4}
12.设α、β、γ为两两不重合的平面,l、m、n为两两不重合的直线,给出下列四个命题:
① 若α⊥γ,β⊥γ,则α∥β;
②若m![]() α,n
α,n![]() α,m∥β,n∥β,则α∥β;
α,m∥β,n∥β,则α∥β;
③若α∥β,l![]() α,则l∥β;
α,则l∥β;
④若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.
其中真命题的个数是
A.1 B.2 C.3 D.4
第II卷 (共90分)
二、填空题:(本大题共6题,每小题4分,共24分.)
13. 已知三角形的三顶点A(2,-1,4),B(3,2,-6),C(-5,0,2),则BC边上的中
线长为 ▲ .
14.计算: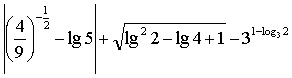 = ▲ .
= ▲ .
15.已知x+2y-3=0,则![]() 的最小值是 ▲ .
的最小值是 ▲ .
16. 正三棱锥P-ABC侧棱长为a,∠APB=30o,D、E分别在PB、PC上,
则△ADE的周长的最小值为 ▲ .
17.若方程![]() 的实根在区间
的实根在区间![]() 内,且
内,且![]() ,
,
则![]() ▲ .
▲ .
18.若函数f(x)=2+log2x的图像与g(x)的图像关于 ▲ 对称,则函数
g(x)= ▲ .(填上正确的命题的一种情形即可,不必考虑所有可能情形)
三、解答题:(本大题共6小题,共66分.解答应写出必要的文字说明,证明过程或演算步骤.)
19.(10分)一个三棱柱木块如图所示,要经过侧面A A1B1B内一点M和直线EF
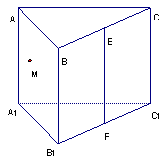 (E、F分别为BC、B1C1的中点)将木块锯开,应怎样画线?并说明理由.
(E、F分别为BC、B1C1的中点)将木块锯开,应怎样画线?并说明理由.
20. (10分)已知f(x)=loga![]() (a>0,a≠1),
(a>0,a≠1),
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性;
(3)判断f(x)单调性并用定义证明.
21. (本小题满分10分)
己知圆C:(x-xo)2+(y-y0)2=R2(R>0)与y轴相切
(1) 求xo与R的关系式
(2) 圆心C在直线l:x-3y=0上,
且圆C截直线m:x-y=0所得的弦长为2![]() ,求圆C方程.
,求圆C方程.
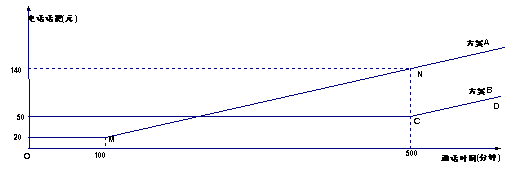
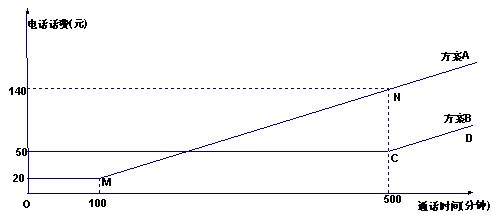
22.(10分)电信局为了满足客户不同需要,设有A、B两种优惠方案,这两种方案应付
话费(元)与通话时间(分钟)之间关系如下图所示(其中MN∥CD).
(1)分别求出方案A、B应付话费(元)与通话时间x(分钟)的函数表达式f(x)和g(x);
(2)假如你是一位电信局推销人员,你是如何帮助客户选择A、B两种优惠方案?
并说明理由.
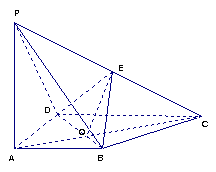
23.(12分)如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,
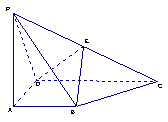 AB∥CD,BA⊥AD,且CD=2AB.
AB∥CD,BA⊥AD,且CD=2AB.
(1)若AB=AD=a,直线PB与CD所成角为450,
①求四棱锥P-ABCD的体积VP-ABCD;
②求二面角P-CD-B的大小.
(2)若E为PC中点,问平面EBD能否垂直于平面ABCD,并说明理由.
24.(本小题14分) 定义:若函数f(x)对于其定义域内的某一数x0,有f(x0)= x0,
则称x0是f(x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意的实数b,函数f(x)恒有两个不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上两个点A、B的横坐标是函数f(x)的不动点,
且A、B两点关于直线y=kx+![]() 对称,求b的最小值.
对称,求b的最小值.
泰州市2005-2006学年度第一学期期末联考
高一数学参考答案
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | C | B | B | D | C | D | A | C | C | B |
二、填空题:
13. 7 14. 0 15. ![]() 16.
16. ![]() a
17. -3
a
17. -3
18. 原点,g(x)=-2-log2(-x) 或x轴,g(x)=-(2+log2x)
或y轴,g(x)=2+log2(-x) 或y=x轴,g(x)=2x-2.(答对相应的 g(x)才给分)
三.解答题:
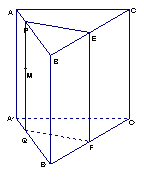 19. 作法:过点M在平面AB1内作PQ∥BB1,
19. 作法:过点M在平面AB1内作PQ∥BB1,
分别交AB,A1B1于P、Q.连结EP、FQ,
则EP、FQ、PQ就是所要画的线.…………5分
证明:∵点M与EF确定平面α,设α![]() 平面AB1=PQ
平面AB1=PQ
又∵E、F分别为BC、B1C1的中点
∴EF∥BB1
∵BB1![]() 平面AB1
平面AB1
∴EF∥平面AB1 ……………………………7分
又∵α![]() 平面AB1=PQ
平面AB1=PQ
∴EF∥PQ
∴PQ∥BB1.…………………………………10分
20. 解:(1)∵![]() >0
>0
∴-1<x<1
故定义域为(-1,1).…………………………3分
(2)∵f(-x)=loga![]() =loga(
=loga(![]() )-1=-loga
)-1=-loga![]() =-f(x)
=-f(x)
∴f(x)为奇函数.……………………………………6分
(3)设g(x)=![]() ,
,
取-1<x1<x2<1,则
g(x1)-g(x2)= ![]() -
-![]() =
=![]() <0
<0
∴g(x)在x![]() (-1,1)为递增函数……………………………8分
(-1,1)为递增函数……………………………8分
∴a>1时,f(x)为递增函数
0<a<1时,f(x)为递减函数……………………………………10分
21. 解:(1)x0=R………………………………………………3分
(2)由圆心C在l:x-3y=0上
可设圆心C(3yo,yo)
∵圆C与y轴相切
∴R=3|yo| ∵d=![]() =
=![]() |yo| ………………………5分
|yo| ………………………5分
∴弦长=2![]() =2
=2![]() ∴2
∴2 ![]() =2
=2![]() ………………………7分
………………………7分
∴yo=![]() 1.
∴R=3. ∴圆C方程: (x-3)2+(y-1)2=9
1.
∴R=3. ∴圆C方程: (x-3)2+(y-1)2=9
或(x+3)2+(y+1)2=9…………………10分
22.
解:⑴f(x)=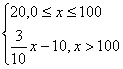 ……………………3分 g(x)=
……………………3分 g(x)= ……………………5分
……………………5分
(1) 当f(x)=g(x)时 ![]() x-10=50
x-10=50
∴x=200.………………………………………………………7分
∴当客户通话时间为200分钟时,两种方案均可………8分
当客户通话时间为0≤x<200分钟,g(x)>f(x),故选择方案A;………9分
当客户通话时间为x>200分钟时,g(x)<f(x),故选方案B.……10分
23.
解:(Ⅰ)∵AB∥CD
∴∠PBA是PB与CD所成角
 即∠PBA=450
即∠PBA=450
∴在直角△PAB中,PA=AB=a
(1)VP-ABCD=![]() ·PA·SABCD=
·PA·SABCD=![]() a3. ……3分
a3. ……3分
(2)∵AB⊥AD,CD∥AB
∴CD⊥AD
又PA⊥底面ABCD
∴PA⊥CD
∴CD⊥平面PAD
∴CD⊥PD
∴∠PDA是二面角P-CD-B的平面角……………5分
在直角△PDA中,∵PA=AD=a
∴∠PDA=450
即二面角P-CD-B为450.…………………………7分
(Ⅱ) 平面EBD不可能垂直于平面ABCD.…………8分
假设平面EBD⊥平面ABCD,
∵PA⊥底面ABCD,且PA![]() 平面EBD
平面EBD
∴PA∥平面EBD
连AC、BD交于O点,连EO
又∵平面EBD![]() 平面PAC=EO
平面PAC=EO
∴PA∥EO
由△AOB∽△COD,且CD=2AB
∴CO=2AO
∴PE:EC=AO:CO =1:2
∴E是PC的三等分点与E为PC中点矛盾
∴平面EBD不可能垂直于平面ABCD.…………………12分
24. 解:(1)f(x)=x2-x-3,由x2-x-3=x,解得 x=3或-1,
所以所求的不动点为-1或3.………………………4分
(2)令ax2+(b+1)x+b-1=x,则ax2+bx+b-1=0 ①
由题意,方程①恒有两个不等实根,所以△=b2-4a(b-1)>0,
即b2-4ab+4a>0恒成立,………………………………6分
则△¢=16a2-16a<0,故0<a<1 …………………………8分
(3)设A(x1,x1),B(x2,x2)(x1≠x2),则kAB=1,∴k=﹣1,
所以y=-x+![]() ,……………………………………9分
,……………………………………9分
又AB的中点在该直线上,所以=﹣+![]() ,
,
∴x1+x2=![]() ,
,
而x1、x2应是方程①的两个根,所以x1+x2=﹣,即﹣=![]() ,
,
∴b=﹣![]() …………………………………………12分
…………………………………………12分
=- =-
=-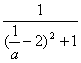
∴当 a=![]() ∈(0,1)时,bmin=-1.………………………………14分
∈(0,1)时,bmin=-1.………………………………14分