高一数学必修一练习题

班级：　　 　 姓名：　　　　 　 座号：　　　 　　评分：　　

1	2	3	4	5	6	7	8	9	10

11．		12．
13．		14．

一、选择题（第小题4分，10小题，共40分）

1.　　　　 六个关系式：①{a,b}{a,b}②{a,b}={b,a}③{0}④0∈{0}⑤∈{0}⑥={0}其中正确的个数为（　 ）

A．6个　　　　　　　　B．5个　　　　　　　　 C．4个　　　　　　　　D．小于4个

2.　　　 下列函数中，有相同图象的一组是（　 ）

A y = x－1, y =　　　 B y=·,　y=

C y = lgx－2, y = lg　　　 D y = 4lgx, y = 2lgx²

3.　　　 已知奇函数 f(x)在[a,b]上减函数，偶函数g(x)在[a,b]上是增函数，则在[-b,-a]（b>a>0）上，f(x)与g(x)分别是（ 　　）

A．f(x)和g(x)都是增函数　　　　 B．f(x)和g(x)都是减函数

C．f(x)是增函数，g(x)是减函数　 D．f(x)是减函数，g(x)是增函数。

4.　　　 方程必有一个根所在的区间是（　　）

A．（1，2）　　　B．(2，3)　　　 C．(e，3)　　　 D．(e,+∞)

5.　　　 下列关系式中，成立的是（　　）

A．　　B．

C．　　　　D．

6.　　　 已知A={x0≤x≤4},B={y0≤y≤2},按照对应法则f不能为从A至B的映射的一个是（　　　　）

A．f:x→y=　　　　　　　　　B．f:x→y=x-2

C．f:x→y=　　　　　　　　　D．f:x→y=x-2

7.　　　 设f()=(x>0)则f(3)的值为（　　 ）

A．128　　　　　B．256　　　　　C．512　　　　　D．8

8.　　　 已知a>0,a≠1则在同一直角坐标系中，函数y=和y=的图象可能是（　 ）

   

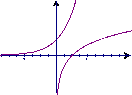
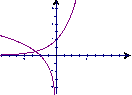
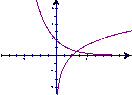
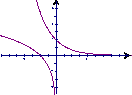
A　　　　　　　　　 B　　　　　　　　　 C　　　　　　　　　 D

9.　　　 若,则实数a的取值范围是（　　）

A．　　 B．　　　C．　　 D．或a>1

10.　　若，，则用p,q表示lg5等于（　　 ）

A．　　　　　　　　　　 B．

C．　　　　　　　　　　D．pq

二、填空题（每小题4分， 4小题，共16分）

11.　　已知函数f (x)在（0，+∞）上为减函数，且在R上满足f (-x)=f (x)，则f (-2)、f (-5)、f (π)三个数的按从小到大依次排列为______________________

12.　　函数y=(x-1)⁰+log_(x-1)(x+x)的定义域是　　　　　　　　　

13.　　设函数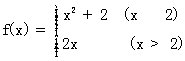若f(x₀)=8则x₀=　　　　　　　　 

14.　　_{若幂函数(mÎZ)的图像与x,y轴无交点，且图像关于原点对称，则m=_______，}

三、计算、证明题

15.　  （8分）计算求值：

 

16.　　（8分）已知在区间(-∞，4]上是减函数，求实数a的取值范围。

 

17.　　（10分）已知函数f(x)=a^x(0<a<1），试判断[f(x₁)+f(x₂)]与f(）的大小，并加以证明。

18.　　（12分）已知函数（a>1,且a≠1）

1)　　　 求函数f(x)的解析式及其定义域

2)　　　 判断函数f(x)的奇偶性

 

19.　　（12分）假设国家收购某种农产品的价格为120元/担，其中征税标准为每100元征8元（称为8个百分点，计划可收购m万担，为了减轻农民负担，决定税率降低x个百分点，预计收购量可增加2x个百分点。（注：1担=50kg）

1)　　　 写出税收y(万元）与x的函数关系；

2)　　　 要使此项税收在税率降低后，不低于原计划的78%，试确定x的范围。

20.　　（14分）设f(x)是定义在R上的偶函数，其图象关于直线x=1对称，对任意x1,x2∈[0，]，都有f(x1+x2)=f(x1)f(x2)。

1)　　　 若f(1)=2，求f()及f()；

2)　　　 证明f(x)=f(x+2),x∈R;

3)　　　 在区间[-，]上写出符合题意的函数解析式，并画出其图象。

高一数学必修一练习题（参考答案）

一、单项选择题：(每题4分，共40分)

二、填空题（每题4分，共16分）

11．f (-5) <f (π)<f (-2)　　12．{xx>0且x≠1}　　 13．或4　　　　14．0或2或4

1	2	3	4	5	6	7	8	9	10
C	C	D	A	A	B	B	D	D	C

三、计算题（64分）

15．解：原式=(3lg2+3lg10)lg5+3(lg2)²+lg(6^-1×0.006)
　　　　　  =[3lg2+3(lg2+lg5)]lg5+3(lg2)²+lg0.001
　　　　　  =3(lg5)²+6lg2·lg5+3(lg2)²-3
　　　　　  =3(lg5+lg2)²-3
　　　　　  =3-3
　　　　　  =0

16．答案：（﹢∞，-3]。提示：对称轴x=1-a，由1-a≥4解得a≤-3。

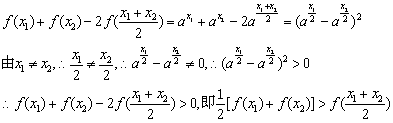17．解：








 

18．（12分）提示：令t=x²-3，换元法
　　　　　　　（1） （-3<x<3)　(2)略

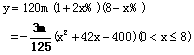19．（12分）
（1）由题设，调节后的税率为（8－x)%，预计可收购m(1+2x%)万担，总金额为120m(1+2x%) 万元，
依题意得

(2)原计划税收为120m·8%万元，依题意得

120m(1+2x%)(8-x)%≥120m·8%·78%
整理得，
而0<x≤8，故0<x≤2
∴税收的范围是0<x≤2。

20．解：

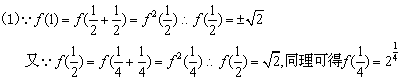
（2）由于图象关于x=1对称，因有f(1+x)=f(1-x),即f(-x)=f(2+x),
又因为f(x)=f(-x)，所以可得f(x)=f(x+2)

(3)图略（可用分段函数）