向量的加法与减法

综合训练卷（120分钟，满分150分）

一、选择题（每题5分，共60分）

1．下列命题中，正确的是（　）

A．　B．

C．　 D．若且，则

2．化简以下各式：（1）；（2）；（3）（4）。结果为零向量的个数是（　）

A．1　　 B．2　　 C．3　 D．4

3．若，且，则的值是（　）

A．必小于5　B．必大于10　C．有可能为0　D．不可能为0

4．若，，则的取值范围是（　）

A．[3，8]　　B．（3，8）　 C．[3，13]　　D．（3，13）

5．在平行四边形ABCD中，若，则必有（　）

A．ABCD是菱形　　 B．ABCD是梯形

C．ABCD是正方形　 D．ABCD是矩形

6．把所有单位向量的起点平移到同一点P，各向量终点的集合构成什么图形（　）

A．点P　　　　　　  B．过点P的一条直线

C．过点P的一条射线　D．以点P为圆心，1为半径的圆

7．下列有关零向量的说法正确的是（　）

A．零向量是无长度，无方向的向量

B．零向量是无长度，有方向的向量

C．零向量是有长度，无方向的向量

D．零向量是有长度，有方向的向量

8．已知，，则的取值范围是（　）

A．[2，12]　B．（2，12）　C．[2，7]　 D．（2，7）

9．“”是“A，B，C是三角形三个顶点的”的（　）

A．充分不必要条件　B．必要不充分条件

C．充要条件　　　　D．既不充分又不必要条件

10．已知两个向量，，则下列说法正确的是（　）

A．向量可以比较大小

B．向量不可以比较大小，但是模可以比较大小

C．当，是共线向量时，可以比较大小

D．当，两个向量中，有一个是零向量时，可以比较大小

11．一艘船从A点出发以的速度向垂直于对岸的方向行驶，同时河水的流速为2km/h。则船实际航行速度大小和方向（用与流速间的夹角表示）

A．大小为4km/h，方向与流速夹角为60°

B．大小为，方向与流速夹角为60°

C．大小为4km/4，方向垂直于对岸

D．大小为，方向垂直于对岸

12．已知向量，，则下列有关与的说法正确的是（　）

A．两者必不相等　　B．>

C．两者可能相等　　 D．无法比较大小

二、填空题（每题4分，共16分）

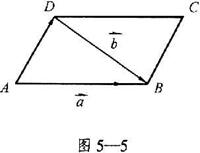
13．如图5—5，在ABCD中，已知=，，则=_______， =_______。

14．已知为与的和向量，且=，则=______，=________。

15．把平行于直线l的所有向量的起点移到l上的点P，则所有向量的终点构成图形_______。

16．已知，是非零向量，则=时，应满足条件________。

三、解答题（共74分）

17．一辆火车向东行驶400km后，改变方向向北行驶400km，求火车行驶的路程及两次位移之和。（10分）

18．飞机按东偏北25°从甲地飞行300km到达乙地，再从乙地按北偏西25°飞行400km到达丙地，求甲丙两地之间的距离。（12分）

19．一艘船以7km/h的速度向垂直于对岸的方向行驶，同时河水的流速为3km/h。求航船实际航行速度大小和方向。（12分）

20．飞机从A地按北偏西75°的飞向飞行400km后到达B地，然后向C地飞行。已知C地从A地西偏南30°的方向处，且A，C两地相距为，求飞机从B地向C地飞行的方向，及B，C两地的距离。（12分）21．已知O为△ABC的外心，H为垂心，求证：。（14分）22．在倾角为30°的斜面上有一块坚直放置的挡板，在挡板和斜面之间有一个重为20N的光滑圆球，求这个球对斜面的压力和对挡板的压力。（14分）

参考答案

一、

1．C2．D3．D4．C5．D6．D7．D8．A9．B10．B11A．12．C

二、

13．—，2—

14．

15．直线l

16．与反向

三、

17．火车两次行驶路程为800km，因为位移是向量，则两次位移之和为 ，方向是东偏北45°。

18．500km，甲、乙两地的连线与乙、丙两地连线垂直。

19．航船实际航速为。方向与河岸夹角为。

20．B地飞向C地方向为东偏南60°，距离为。

21．略

22．球对斜面压力为，对挡板的压力为

[解题点拨]

1．选项D 中：当=时，对任意向量（非零），，都有∥，∥但此时与不一定平行。

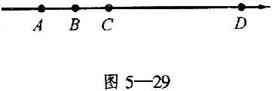
3．当A，B，C，D四点位置如图5—29所示时，>5，排除A。

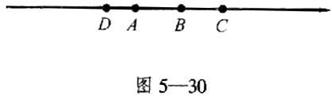
当A，B，C，D四点如图5—30时：<10，排除B。

假设=0，则A、D两点重合，

由∴

4．∵当，同向时，=8-5=3；当，反向时，=8+5=13；，当，不平行时，3<<13。结上可知3≤BC≤13

∴应选C

注意：本题要根据问题的实际作好分类讨论，作到分类不漏不重。

7．零向量是特殊向量，符合向量的定义，零向量的长度为0，零向量的方向是任意的。

8．（1）若与共线：

①与同向时：

②与反向时：

（2）若与不共线，则由向量的可平移性及向量的三角形法则知：

11．速度是向量，利用向量加法的平行四边形法则或三角形法则求解。

12．分“与共线与不共线”两种情况进行讨论，与共线时又分同向与异向进行讨论。当与共线且同向时：若≥，则=。

以下16题类似求解。

14．利用向量加、减法的三角形法则求解。

20．准确画出图形后，经分析、计算知：△ACB是等腰直角三角形，故

21．由图形可知，与，，之间不存在表面上的联系，要借助圆来找到它们的内在联系，由三角形法则可知=+，而H总是△ABC的垂心，说明AH与BC垂直，利用这一关系来寻找与，间的联系。△ABC是圆O的内接三角形，可连接OB并延长它交圆于D点，由圆的知识可知DC与BC垂直，则与的方向相同。同时由图可知与的方向相同，四个点A，H，D，C可以构成平行四边形，与方向相同，大小相等是相等向量，而=—，向量与方向相反，大小相等是相反向量，=+。通过图形的分析，可以找出四个向量之间的联系，可以解决问题。本题在分析图形的基础上，借助向量的方法，解决几何问题，充分体现了数形结合的思想，是向量考查中的一个难点。

22．本题考查向量加法、减法在实际物理问题中的运用。力是一个既有大小又有方向的量，它是一个向量。力的分解也就是向量的分解。已知了重力，即已知了两个向量的和，利用直角三角形求两个向量的大小。先画出草图，利用平面几何的知识分析直角三角形的内角，再要求直角三角形中斜边与直角边的关系，求出两个分力的大小。高考在考查向量加、减法的运算中，一般不会直接考查，会借助一些实际的应用问题来考查向量的加、减法。