2005－2006学年度上学期

高中学生学科素质训练

新课标高一数学同步测试（2）—第一单元（集合）

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（每小题5分，共50分）.

1．方程组的解构成的集合是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A． 　　　　　B．　　　　  C．（1，1）　　　　　　D．

2．下面关于集合的表示正确的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　①；

②；

③=；

④；

　　　 A．0　　　　  　　　 B．1　　　　　　　　　　　　C．2 　　　　　　　　　　　D．3

3．设全集，，，那么∩=　　　　　　　　　　　　　　　　　　　　（　　）

　　A．　　  　　　　　　B．{（2，3）}　　　　 C ．（2，3） 　　　　　D．

4．下列关系正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．

　B．=

　C．

　D．=

5．已知集合A中有10个元素，B中有6个元素，全集U有18个元素，。设集合有个元素，则的取值范围是　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．，且 　　　　　　　　　 B．，且

C．，且　　 　　　　　　　D．，且

6．已知集合 ，，

，则的关系　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．　　　B．　　　C．　　 D．

7．设全集，集合，集合，则　　　　　　　　　（　  ）

　　A．　　　　　　　  　　　　　 B．

　　C．　　　　　  　　　　　D．

8．已知，，且，则a的值（　 ）

A．1或2　　　　　　　　 B．2或4　　　　　　　　　C．2　　　　　　　　 D．1

9．满足的集合共有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．7组　　　　  　B．8组　　 　　　　　 C．9组　 　　　　D．10组

10．下列命题之中，U为全集时，不正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．若= ，则

B．若= ，则= 或=

C．若= ，则

D．若= ，则

二、填空题：请把答案填在题中横线上（每小题6分，共24分）.

11．若，，用列举法表示B　　　　　  　　.

12．设集合，，则　　　　  .

13．含有三个实数的集合既可表示成，又可表示成，则　　　　  .

14．已知集合，，那么集合　　　　  ，　　　　  ，　　　　  .

三、解答题：解答应写出文字说明、证明过程或演算步骤(共76分).

15．（12分）数集A满足条件：若，则.

　　　 ①若2，则在A中还有两个元素是什么；

　　　 ②若A为单元集，求出A和.

16．（12分）设，，.

　　　 ①=，求a的值；

　　　 ②，且=，求a的值；

　　　 ③=，求a的值；

17．（12分）设集合，，，求实数a的值.

18．（12分）已知全集，若，，，试写出满足条件的A、B集合.

19．（14分）在某次数学竞赛中共有甲、乙、丙三题，共25人参加竞赛，每个同学至少选作一题。在所有没解出甲题的同学中，解出乙题的人数是解出丙题的人数的2倍；解出甲题的人数比余下的人数多1人；只解出一题的同学中，有一半没解出甲题，问共有多少同学解出乙题？

 

20．（14分）集合满足=A，则称（）为集合A的一种分拆，并规定：当且仅当时，（）与（）为集合A的同一种分拆，则集合A={}的不同分拆种数为多少？

参考答案（2）

一、ACBCA　　BCCCB

二、11．{4，9，16}；　　12．{}；　 13．－1；　 14．或；；或

三、15． 解：①和；

②（此时）或（此时）。

16．解：①此时当且仅当，有韦达定理可得和同时成立，即；

②由于，，故只可能3。

此时，也即或，由①可得。

③此时只可能2，有，也即或，由①可得。

17．解：此时只可能，易得或。

当时，符合题意。

当时，不符合题意，舍去。

故。

18．分析：且，所以{1，2}A，3∈B，4∈B，5∈B且1B，2B；

但，故{1，2}A，于是{1，2}A{1，2，3，4，5}。

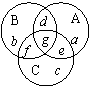19．分析：利用文氏图，见右图；

可得如下等式　；

；；

；联立可得。

20．解：当＝时，=A,此时只有1种分拆；

当为单元素集时，=或A，此时有三种情况，故拆法为6种；

当为双元素集时，如={}，B=、、、，此时有三种情况，故拆法为12种；

当为A时，可取A的任何子集，此时有8种情况，故拆法为8种；

总之，共27种拆法。