2005-2006学年度上学期
高中学生学科素质训练
高一数学同步测试(5)—反函数与函数的单调性
说明:本试卷分第I卷和第II卷两部分,第I卷60分,第II卷90分,共150分;答题时间150分钟.
第Ⅰ卷(共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数![]() 的反函数是 ( )
的反函数是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.已知函数![]() 有反函数,且
有反函数,且![]() 的图象经过点
的图象经过点![]() ,则下列函数中可能
,则下列函数中可能
是![]() 的反函数的一个函数是
( )
的反函数的一个函数是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.设函数![]() 为奇函数,
为奇函数,![]() 则
则![]() ( )A.0 B.1 C.
( )A.0 B.1 C.![]() D.5
D.5
4.函数![]() 在区间[1,2]上存在反函数的充分必要条件是 ( )
在区间[1,2]上存在反函数的充分必要条件是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若f(x)=-x2+2ax与![]() 在区间[1,2]上都是减函数,则a的值范围是 ( )
在区间[1,2]上都是减函数,则a的值范围是 ( )
A.![]() B.
B.![]() C.(0,1) D.
C.(0,1) D.![]()
6.函数![]() 的反函数为 ( )
的反函数为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.已知函数![]() 的反函数就是
的反函数就是![]() 本身,则
本身,则![]() 的值为 ( )
的值为 ( )
A.![]() B.1 C.3 D.
B.1 C.3 D.![]()
8.设偶函数f(x)的定义域为R,当x![]() 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f(![]() ),f(-3)的大小关系
),f(-3)的大小关系
是 ( )
A.
f(![]() )>f(-3)>f(-2) B.
f(
)>f(-3)>f(-2) B.
f(![]() )>f(-2)>f(-3)
)>f(-2)>f(-3)
C.
f(![]() )<f(-3)<f(-2) D.
f(
)<f(-3)<f(-2) D.
f(![]() )<f(-2)<f(-3)
)<f(-2)<f(-3)
9. 函数![]() 存在反函数,则方程
存在反函数,则方程![]() ( )
( )
A.有且只有一个实数根 B.至少有一个实数根
C.至多有一个实数根 D.没有实数根
10.已知f(x)在区间(-∞,+∞)上是增函数,a、b∈R且a+b≤0,则下列不等式中正确的是 ( )
A.f(a)+f(b)≤-f(a)+f(b) B.f(a)+f(b)≤f(-a)+f(-b)
C.f(a)+f(b)≥-f(a)+f(b) D.f(a)+f(b)≥f(-a)+f(-b)
11.点(2,1)既在函数f(x)=![]() 的图象上,又在它的反函数的图象上,则适合条件的数组(a,b)有 ( )
的图象上,又在它的反函数的图象上,则适合条件的数组(a,b)有 ( )
A.1组 B.2组 C.3组 D.4组
12.设![]() 是函数f(x)=
是函数f(x)=![]() 的反函数,则下列不等式中恒成立的是 ( )
的反函数,则下列不等式中恒成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(共90分)
二、填空题:本题共4小题,每小题4分,共16分.把答案填在题中的横线上.
13.已知函数![]() 是奇函数,当
是奇函数,当![]() 时,
时, ![]() ,设
,设![]() 的反函数是y=g(x),则g(-8)=__ .
的反函数是y=g(x),则g(-8)=__ .
14.函数f(x) = ax2+4(a+1)x-3在[2,+∞]上递减,则a的取值范围是__ .
15.已知f(x) = 4x-2x+1 ,求f-1(0)的值___________________.
16.若f(x)=-x2+2ax与![]() 在区间[1,2]上都是减函数,则a的值范围是________.
在区间[1,2]上都是减函数,则a的值范围是________.
三、解答题:本大题共6小题,共74分.解答应写出必要的文字说明、证明过程及演算步骤.
17.用定义证明:函数![]() 在
在![]() 上是增函数. (12分)
上是增函数. (12分)
18.设f(x)是R上的奇函数 ,且当x![]() [0,+ ∞
[0,+ ∞![]() 时,f(x)=x(1+
时,f(x)=x(1+![]() ),求f(x)在(-
),求f(x)在(- ![]() ,0)上的表达式和在R上的表达式.(12分)
,0)上的表达式和在R上的表达式.(12分)
19. 讨论函数f(x)=![]() ,在-1<x<1上的单调性. (12分)
,在-1<x<1上的单调性. (12分)
20.f(x)为偶函数,g(x)为奇函数且f(x)+g(x)=![]() ,求f(x),g(x). (12分)
,求f(x),g(x). (12分)
21.定义在(-1,1)上的奇函数f(x)是减函数且f(1-a)+f(1-a2)<0,求实数a的取值围. (12分)
22.已知函数f(x)=![]() ,x∈[1,+∞
,x∈[1,+∞![]() (14分)
(14分)
(1)当a=![]() 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若对任意x∈1,+∞![]() ,f(x)>0恒成立,试求实数a的取值范围.
,f(x)>0恒成立,试求实数a的取值范围.
|
2005-2006学年度上学期
高中学生学科素质训练
高一数学同步测试(5)—反函数与函数的单调性答案
一、选择题
1.A 2.B 3.C 4.D 5.D 6.B 7.D 8.A 9.C 10.B 11.A 12.C
二、填空题
13. ![]() 14.
14. ![]() 15. 1. 16.
15. 1. 16. ![]() .
.
三、解答题
17.任给![]() 且
且![]() ,
,
则![]()
![]()
![]() =
=![]()
![]()
=![]() .
.
![]() 且
且![]() ,
,![]() .
.
![]() 即有
即有![]() ,
,
![]()
![]()
![]() ,
,
![]() , 即
, 即![]() 在
在![]() 上是增函数.
上是增函数.
18.设x![]() (-
(-![]() ,0),则-x
,0),则-x ![]() (0,+
(0,+ ![]() ),∴f(-x)=-x(1-
),∴f(-x)=-x(1-![]() )。
)。![]() f(x)是R上的奇函数,
f(x)是R上的奇函数,
∴
f(x)=x(1-![]() )(x
)(x![]() (-
(- ![]() ,0)),f(x)在R上的表达式是f(x)=x(1+
,0)),f(x)在R上的表达式是f(x)=x(1+![]() ).
).
19.设-1<x1<x2<1,则f(x2)-f(x1)=![]()
∴当a>0时,f(x)在(-1,1)上为减函数;当a<0时,f(x)在(-1,1)上为增函数.
20.![]() f(x)+g(x)=
f(x)+g(x)=![]() , ∴
, ∴![]() f(-x)+g(-x)=
f(-x)+g(-x)= ![]() 即f(x)-g(x)=-
即f(x)-g(x)=- ![]() ,将
,将
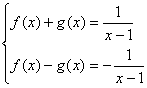 联立解得f(x)=
联立解得f(x)=![]() .
.
21.![]() f(x)在(-1,1)上为奇函数且为减函数,
f(x)在(-1,1)上为奇函数且为减函数, ![]()
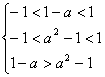 ,则a
,则a![]() (0,1).
(0,1).
22.(1)当a=![]() 时,f(x)=x+
时,f(x)=x+![]() +2,x∈[1,+∞). 设x2>x1≥1,则f(x2)-f(x1)=x2+
+2,x∈[1,+∞). 设x2>x1≥1,则f(x2)-f(x1)=x2+![]() =(x2-x1)+
=(x2-x1)+![]() =(x2-x1)(1-
=(x2-x1)(1-![]() ).
).
∵x2>x1≥1,∴x2-x1>0,1-![]() >0,则f(x2)>f(x1)
>0,则f(x2)>f(x1)
可知f(x)在[1,+∞![]() 上是增函数.
上是增函数.
∴f(x)在区间[1,+∞![]() 上的最小值为f(1)=
上的最小值为f(1)=![]() .
.
(2)在区间[1,+∞![]() 上,
上,
f(x)=![]() >0恒成立
>0恒成立![]() x2+2x+a>0恒成立
x2+2x+a>0恒成立
设y=x2+2x+a,x∈1,+∞),由y=(x+1)2+a-1可知其在[1,+∞)上是增函数,
当x=1时,ymin=3+a,于是当且仅当ymin=3+a>0时函数f(x)>0恒成立.故a>-3.

