2005高一（上）深圳实验学校数学期末复习（二）

一、选择题

1．给出下列四个命题：

（1）垂直于同一条直线的两条直线平行；

（2）垂直于同一条直线的两个平面平行；

（3）垂直于同一平面的两条直线平行；

（4）垂直于同一平面的两平面平行。

其中正确命题的个数为

（A）1　　　　　  （B）2　　　　　  （C）3　　　　　  （D）4

2．已知平面和直线，则在平面内至少有一条直线与直线

（A）平行　（B）垂直　（C）相交　（D）以上都有可能

3．已知直线l⊥平面α，直线m平面β，有下面四个命题：

①；②；③；④，其中正确的两个命题的序号是

（A）①与②　　　　　　（B）③与④ 　　　　　　　（C）②与④　　　　　　（D）①与③

4．对于相异直线a，b和不重合平面∥b的一个充分条件是

（A）a∥, b∥　　　　　　　　　　　　　 （B）a∥，b∥，∥

（C）a ⊥，b ⊥，∥　　　　 （D）⊥，a ⊥，b ∥

5．有一块直角三角板ABC，∠A=30°，∠B=90°，BC边在桌面上，当三角板所在平面与桌面成45°角时，AB边与桌面所成的角等于

（A）　 （B）　　　　 （C）　　　　 （D）

6．从P点引三条射线PA，PB，PC，每两条射线夹角为60°，则平面PAB和平面PBC所成二面角正弦值为　　　

（A）　　　　　　（B）　　　　（C）　　　　（D）

7．已知长方体ABCD－A₁B₁C₁D₁中，AB=BC=4，CC₁=2，则直线BC₁和平面DBB₁D₁所成角的正弦值为

（A）　　　　　　　（B）　　　　（C）　　　 （D）

8．等边△ABC的边长为a，将它沿平行于BC的线段PQ折起，使平面APQ⊥平面BPQC，若折叠后AB的长为d，则d的最小值是

（A）　　　　　　 （B）　　  （C）　　　　 （D）

9．如图，在正三棱锥P—ABC中，M、N分别是侧棱PB、PC的中点，若截面AMN⊥侧面PBC，则此三棱锥的侧棱与底面所成角的正切值是

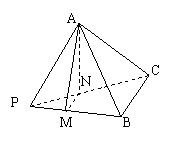（A）　　　 （B）　　（C）　　 （D）

10．正四棱锥P—ABCD的侧棱长和底面边长都等于，

有两个正四面体的棱长也都等于.当这两个正四面体各

有一个面与正四棱锥的侧面PAD，侧面PBC完全重合时，得到一个新的多面体，该多面体是

（A）五面体　　  （B）七面体　　 （C）九面体　　  （D）十一面体

11．一个正方体纸盒展开后如图，在原正方体纸盒中有下列结论

①AB⊥EF　②AB与CM成60°　③EF与MN是异面直线　④MN//CD

其中正确的是　

（A）①②　　　　　　　 （B）③④　　　 （C）②③　　　 （D）①③

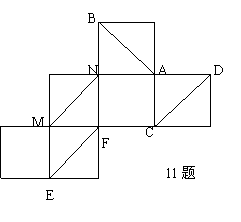12．正四面体的四个顶点都在一个球面上，且正四面体的高为4，则球的表面积为

（A）（B）18　　（C）36　　　 （D）

二、填空题

13．三棱锥三条侧棱两两互相垂直，三个侧面积分别为1.5cm²、2 cm²、及6 cm²，则它的体积为　　　　　  ．

14．空间四边形ABCD中，AB=CD，且AB与CD成60°角，E、F分别为AC，BD的中点，则EF与AB所成角的度数为　　　　　　 ．

15．在150°的二面角内，放入一半径为4的球，分别与两个半平面相切于A、B两点，则A、B间的球面距离为　　　　   ．

16．在正三棱锥P—ABC中，D为PA的中点，O为△ABC的中心，给出下列四个结论：①OD∥平面PBC；　②OD⊥PA；③OD⊥BC；　④PA=2OD.

其中正确结论的序号是　　　　　　　　  ．

三、解答题

17．如图，MN，A，CMN，且∠ACM＝，为，AC＝1，求A点到的距离。

18．试构造出一个三棱锥S—ABC，使其四个面中成直角三角形的个数最多，作出图形，指出所有的直角，并证明你的结论。

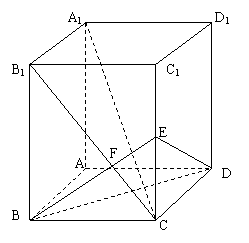19．已知长方体AC₁中，棱AB＝BC＝3，棱BB₁＝4，连结B₁C，过B点作B₁C的垂线交CC₁于E，交B₁C于F.

（1）求证A₁C⊥平面EBD；

（2）求二面角B₁—BE—A₁的大小.

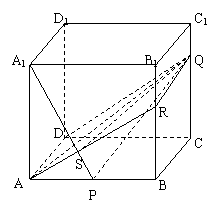
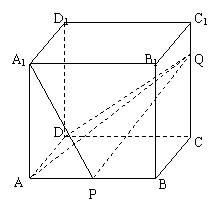20．如图棱长是1的正方体，P、Q分别是棱AB、CC₁上的点，且.

（1）求证：A₁P⊥平面AQD；

（2）求直线PQ与平面AQD所成角的正弦值.

21．如图，四棱锥P—ABCD的底面是正方形,PA⊥底面ABCD，PA=AD=2，点M、N分别为棱PD、PC的中点.

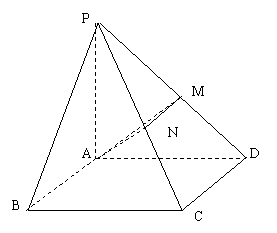（1）求证：PD⊥平面AMN；

（2）求三棱锥P—AMN的体积；

（3）求二面角P—AN—M的大小.

22．如图，四棱锥P—ABCD中，侧面PDC是边长为2的正三角形且与底面ABCD垂直，且ABCD为菱形.

（1）求证：PA⊥CD；

（2）求异面直线PB和AD所成角的余弦值；

（3）求二面角P—AD—C的正切值.

参考答案

一、选择题

1 B  2B　3 D　4 C  5C　6A　7C  8B　9C　10A  11D　12C

二、填空题

13．2；14．60°或30°；15．；16．③，④

17．解：作AH⊥于H，则AH是A点到的距离，

作HO⊥MN于O，连结AO，则∠AOH＝60°，

在直角三角形AOC中，AO＝，在直角三角形AOH中，AH＝．

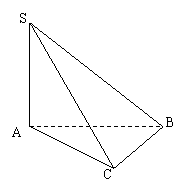18．解：如图，SA⊥平面ABC，∠ABC＝，

则∠SAC＝∠SAB＝，

又AB⊥BC，所以BC⊥SB，

所以∠SBC＝，

即四个面SAB，SAC，SBC，ABC为直角三角形。

19．解：（1）连结AC，则AC⊥BD，又AC是A₁C在平面ABCD内的射影

∴A₁C⊥BD；又∵A₁B₁⊥面B₁C₁CB，且A₁C在平面B₁C₁CB内的射影B₁C⊥BE，

∴A₁C⊥BE，

∵BD∩BE=B，∴A₁C⊥面EBD.

（2）连结A₁F，∵BE⊥B₁C，BE⊥A₁B₁，∴BE⊥平面A₁B₁C，

∴∠B₁FA₁就是二面角B₁—BE—A₁的平面角.

，

所以二面角B₁—BE—A₁的大小 等于．

20（1）平面AQD与侧棱B₁B的交点是R，

　　　 显然 在正方形ABB₁A₁中

由

　　　 所以,

　　　 又AA₁⊥平面ABCD，AP⊥AD，得A₁P⊥AD，A₁P⊥平面AQD

（2）设A₁P与AR交于点S，连接SQ，则即为PQ与平面AQD所成角.

 在Rt△PQS中，，，

即直线PQ与平面AQD所成角的正弦值是．

21（1）证明：∵ABCD是正方形，∴CD⊥AD ，

∵PA⊥底面ABCD　，∴AD是PD在平面ABCD内的射影，

∴CD⊥PD ，在△PCD中，M、N分别是PD、PC的中点，

则MN//CD，∴MN⊥PD，在△PAD中，PA=AD=2，M为PD的中点.

∴AM⊥PD　则PD⊥平面AMN ．

（2）解：∵CD⊥AD，CD⊥PD　 ∴CD⊥平面PAD．

  ∵MN//CD，∴MN⊥平面PAD，又∵AM平面PAD　∴MN⊥AM，∠AMN=90°.

在Rt△PAD中，PA=AD=2，M为PD的中点，∴AM=PM=.　 又MN=CD=1，

 ．∵PM⊥平面AMN，

∴PM为三棱锥P—AMN的高，．

　 （3）解：作MH⊥AN于H，连结PH，

∵PM⊥平面AMN，∴PH⊥AN，

∴∠PHM为二面角P—AN—M的平面角，

∵PM⊥平面AMN，∴PM⊥MH．

在Rt△AMN中，，

在Rt△PMH中，，

所以，　即二面角P—AN—M的大小为60⁰．

22．解（1）证明，取CD中点O，连OA、OP，　　∵面PCD⊥面ABCD， PO⊥CD，

　 ∴PO⊥面ABCD，　 即AO为PA在面ABCD上的射影，　 又在菱形ABCD中，∠ADC=60°，O为CD中点∴AO⊥CD，　∴PA⊥CD．

（2）显然∠PBC是PB和AD所成的角，其余弦值为 ．

（3）由O引OG⊥AD于G，连PG，则PG⊥AD，　∠PGO为二面角P—AD—C为平面角，，即二面角P—AD—C的正切值为2．