《正弦定理、余弦定理、解斜三角形》

一、复习要求 ：

1．  掌握正弦、余弦定理，能运用知识解斜三角形。

2．  用正弦、余弦定理判断三角形的形状。

二、知识点回顾

（1）　　　 正弦定理：（2R为三角形外接圆直径），

（为三角形面积），其他形式： a ：b ：c =　sinA　：sinB　：sinC

　　　　　　　　　　　　　　　  a=2RsinA,　b=2RsinB , c=2RsinC

(2) 余弦定理：a²=b²+c²-2bccosA,(可按a,b,c,a轮换得另二式)

余弦定理变式： , (轮换得另二式)

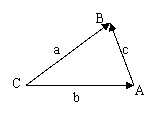
余弦定理向量式：如图　a=b+ c　,  c= a – b

c²=c²=a-b²=(a-b)²=a²+b²-　2﹒a﹒b

　　　　　　　　 =a²+b² - 2abcosC

(其中｜a=a,b=b,c=c)

三、典型例题分析：

 例1：在三角形ABC中，若C=3B，求的范围

分析：角边比转化，可用正弦定理

解：

 A+B+C=180⁰　，C=3B， ４Ｂ<１８０^０，０^０<Ｂ<４５^０，

　　　　１<４cos²B-1<3　　故　

练习1：在ABC中，若sinA=2cosBsinC,则ABC的形状是　　　　

例2：在ABC中，已知4sinBsinC=1, B>C ,且b²+c² =a²+bc, 求A，B，C。

解： ， 　 A=60⁰　又 4sinBsinC=1

4sinBsin(120⁰-B)=1

　　 2B=30⁰  或210⁰

　B>C　, 2B=210⁰　 即 B=105⁰

A=60⁰　　B=105⁰ C=15⁰

练习2：在ABC中，2B=A+C　且tanAtanC=2+　求（1）A、B、C的大小

（2）　　　 若AB边上的高CD=4，求三边a、b、c

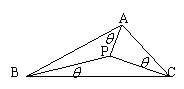例３：如图，已知Ｐ为ABC内一点，且满足∠ＰＡＢ＝∠ＰＢＣ＝∠ＰＣＡ＝

求证cot=cotA+cotB+cotC

解：在ABC中，

＝

同理　

sinAsinBsinCcos=sinAsinBcosCsin+sin²C sin

四：作业

１．在ABC中，a+b=　　　求边c的长

２．在ABC中，Ｓ是它的面积，a,b是它的两条边的长度，Ｓ＝

求这个三角形的各内角．

３．已知圆Ｏ的半径为Ｒ，它的内角三角形ＡＢＣ中，２Ｒ（sin²A-sin²C）=

成立，求三角形ＡＢＣ的面积Ｓ的最大值．