舟山中学2005学年第一学期高一理科实验班期终考试

数学试卷

一．选择题（本大题共12小题，每小题5分，共60分）：

1．设集合A={xx²<a}，B={xx<2}，若A∩B=A，则实数a的取值范围是········· （　　 ）

(A)a<4　　　　　　　　　　 (B)a≤4　　　　　　　　　　　(C)0<a≤4　　　　　　　　　(D)0<a<4

2．数列{a_n}满足：a₁，a₂-a₁，a₃-a₂，…，a_n-a_n-1，…是首项为1，公比为的等比数列， 那么a_n=　（　　 ）

(A)　　　　　　(B)　　　　　 (C)　　　　　 (D)

3．已知{a_n}为等差数列，{b_n}为等比数列，其公比q¹1，且b_i>0(i=1,2,3,…n)，若a₁=b₁，

　a₁₁=b₁₁，则······························································································· （　　 ）

(A)a₆=b₆　　　　　 (B) a₆>b₆　　　　　　 (C) a₆<b₆　　　　(D) a₆>b₆ 或a₆<b₆

4．设f (x)=ax²+bx+c(a>0)满足f (1+x)=f (1-x)，则f (2^x)与f (3^x)的大小关系为·· （　　 ）

(A) f (3^x)≥ f (2^x)　　 (B) f (3^x)≤ f (2^x)　　　　(C) f (3^x)< f (2^x)　　　　 (D)不确定

5．已知数列{a_n}的前n项和为S_n=1-5+9-13+17-21+…+(-1)^n-1(4n-3)，则S₁₅+S₂₂-S₃₁

的值是····································································································· （　　 ）

(A)13　　　　　　　　　　　 (B)46　　　　　　　　　　　　 (C)-76　　　　　　　　　　　　(D)76

6．若不等式x²-log_mx<0在区间(0，)内恒成立，则实数m的取值范围是······· （　 　）

(A) m≥　　　　　 (B)0<m≤　　　　　　　(C)0<m<　　　　　　 (D) ≤m<1

7．函数的部分图象如图所示，则函数表达式为（　　　）

（A） （B）

（C） （D）

 

8．若{a_n}是等差数列，首项a₁>0，a₂₀₀₃+a₂₀₀₄>0，a₂₀₀₃·a₂₀₀₄<0，则使前n项和S_n>0

成立的最大自然数n是············································································· （　　 ）

(A)4005　　　　　　　　　 (B)4006　　　　　　　　　　　(C)4007　　　　　　　　　　 (D)4008

9.已知函数是R上的增函数，A（0，-1）、B（3，1）是其图象上的两点，则 的解集是（　）

A、 　B、　 C、　　 D、

10.若关于的方程有实解,则实数的取值范围是（　　）

A、(-,-) 　　B、[ 　　　 C、] 　　　　D、

11．函数的单调增区间为

A. 　　　　B.

C. 　　　　D.

12.已知，则的最大值等于

A. 　　　B.　　C. 　　D.

二．填空题(每小题4分，共16分)

13．函数，为增区间是　　　　 。

14． 函数的反函数　　　　　 。

15．已知正项数列，，()，则数列的前项和　　　　　　。

16．函数的值域为　　　　  。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

舟山中学2005学年第一学期高一理科实验班期终考试

数学答卷

　　　　　  班级　　　　学号　　　　　　姓名　　　　　　

一．选择题

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二．填空题

13．　　　　 　　。14　　　　　　　　　。15　　　　　　　　。16　　　　　　。

三．解答题（本大题共８小题，满分74分）：

17．（本小题满分８分）

设集合A={yy=，xÎ[0,3]}，B={yy²-(a²+a+1)y+a³+a≥0}，若

A∩B=Æ，求实数a的取值范围。

　　　

18．（本小题满分10分）

已知求的定义域、值域、周期，并判断它的奇偶性。

19（本小题满分1０分）

某沙漠地区经过人们的改造，到2005年底，将1万亩沙漠面积的30﹪变为绿洲，计划从2006年起，每年将剩余沙漠的面积的16﹪改造为绿洲，同时上一年绿洲面积的4﹪被侵蚀，又变成了沙漠。从2006年开始，

(1)　  经过年后，该地区的绿洲面积为多少万亩？

(2)　  至少经过多少年的努力，才能使该地区沙漠绿化率超过60﹪？

20（本小题满分８分）若求的取值范围。

21． (本小题满分8分)证明：设则

22．(本小题满分1０分)已知定义在[-1,1]上的函数,对任意[-1,1]有,若[-1,1],,>0。⑴判断函数在[-1,1]是增函数还是减函数并证明你的结论；⑵解不等式。

23．（本小题１０分）

设等比数列的公比为，前项和为，

⑴求的取值范围；

⑵设，记的前项和为，试比较与的大小。

　　

24．(本小题满分1０分)

已知数列中，且其中。

(1)求， (2)求的通项公式。

 附加题（6分）．

在锐角三角形ABC中，A、B、C是其三个内角，求证：

舟山中学2005学年第一学期高一理科实验班期终考试答案：

一．选择题：ＢＤＢＡＣ；ＤＡＢＣＣ；ＡＣ

二．填空题：；；；

三．解答题　

　17．　　　　　　　

  18．定义域;值域　

周期,奇偶性为偶函数。　　

  19．解：（1）设从2006年起（2006年为第一年）该地区的绿洲面积为，由题意知，　，可求

　　　　 （2）至少经过5年。

20．　　　

21．证明略。

22．（1）证明略；（2）　

23．（1）且　　　　

　 （2）或时，；

且时，　；

或，　　

24．（1）　

　 （2）　　　　　

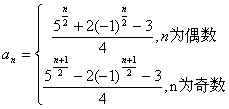
附加题略。