江苏省高淳高级中学05/06学年第二学期第二次阶段考试
高一数学试题
一、选择题(本大题共10小题,每小题5分,共50分)
1.下列各三角函数式中,大于零的是 ( )
A.sin(-1) B.cos2 C.tan3 D.sin400°
2.下列函数中以周期为π的奇函数的为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.已知a、b、c都是非零向量,则下列结论正确的是 ( )
A.(a·b)c=a(b·c) B.0·a=0
C.若a·b>0,则向量a,b的夹角为锐角 D.若 a+b = a-b ,则a⊥b
4.函数y=3cos(3x+![]() )的图象是由y=3cos3x的图象平移而得,平移方法是( )
)的图象是由y=3cos3x的图象平移而得,平移方法是( )
A.向左平移![]() 个单位长度 B.向左平移
个单位长度 B.向左平移![]() 个单位长度
个单位长度
C.向右平移![]() 个单位长度 D.向右平移
个单位长度 D.向右平移![]() 个单位长度
个单位长度
5.cos600°的值是 ( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
6.使sinx≤cosx成立的x一个变化区间是 ( )
A.[-![]() ,
,![]() ] B.[-
] B.[-![]() ,
,![]() ] C.[-
] C.[-![]() ,
,![]() ] D.[0,π]
] D.[0,π]
7.已知![]() =(-3,-1),
=(-3,-1),![]() =(1,1),且点P(x,2)在线段MN的中垂线上,则x等于
( )
=(1,1),且点P(x,2)在线段MN的中垂线上,则x等于
( )
A.-2 B.-1 C.0 D.3
8.下列三角函数不等关系正确的是 ( )
A.cos2<cos3 B.sin1>sin2 C.sin2<tan2 D.tan1>tan10
9.已知△ABC为钝角三角形,其中∠C为钝角,则下列结论正确的是 ( )
A.tanAtanB<1 B.sinA+sinB+sinC<0
C.tanAtanBtanC>0 D.cosA+cosB+cosC<0
10.已知O为原点,点A、B的坐标分别为(a,0),(0,a)其中常数a>0,点P在线段AB上,且![]() (0≤t≤1),则
(0≤t≤1),则![]() 的最大值为
( )
的最大值为
( )
A.a B.2a C.3a D.a2
二、填空题(本大题共6小题,每小题5分,共30分)
11.若tan(α+![]() )=-3,则
)=-3,则![]() =
.
=
.
12.已知△ABC三个顶点的坐标为:A(-2,-3),B(-1,-6),C(19,4),
则△ABC的形状是 .
13.已知一物体在共点力f1=(1,1),f2=(-2,0)的作用下产生位移s=(1,0),则共点力对物体做的功W= .
14.cos83°+cos37°-cos23°的值是 .
15.已知a=(2,1),b=(-1,3),且a+b与2a-kb共线,则实数k= .
16.关于函数f(x)=4sin(2x+![]() ),x∈R,有下列命题:
),x∈R,有下列命题:
①由f(x1)=f(x2)=0,可得x1-x2是π的整数倍;
②y=f(x)的表达式可改写为y=4cos(2x-![]() );
);
③y=f(x)的图象关于点(-![]() ,0)对称;
,0)对称;
④y=f(x)的图象关于直线x=-![]() 对称.
对称.
其中正确命题是 (填写正确结论的序号).
三、解答题(本大题共5小题,每小题14分,共70分)
17.(Ⅰ)化简: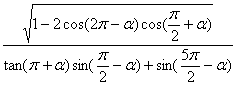 (其中α为第一象限角);
(其中α为第一象限角);
(Ⅱ)求值:![]() .
.
18.已知点A(3,0),B(0,3),C(cosθ,sinθ).
(Ⅰ) 若![]() ·
·![]() =-1,求sin2θ的值;
=-1,求sin2θ的值;
(Ⅱ) 若![]() +
+![]() =
=![]() ,且θ∈(0,π),求
,且θ∈(0,π),求![]() 与
与![]() 的夹角.
的夹角.
19.已知函数f(x)=2![]() +2
+2![]() a
a![]()
![]() -2
-2![]() ,且f(
,且f(![]() )=3.
)=3.
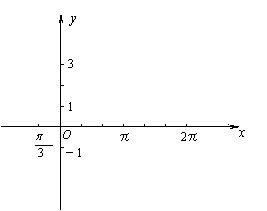 (Ⅰ) 求实数a的值;
(Ⅰ) 求实数a的值;
(Ⅱ) 指出f(x)的单调减区间及其对称中心;
(Ⅲ) 用五点法画出函数f(x)的简图.
20.已知△ABC中,E、M分别在AB、BC上,且BM=2MA,BE=EC,N为AE中点.
(Ⅰ) 求证:C、N、M三点共线;
(Ⅱ) 若AB=2AC,∠BAC=60°,AB的垂线CD交AE于点P,求![]() 的大小.
的大小.
 |
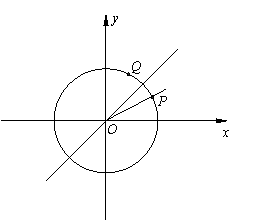
21.如图,已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.
(Ⅰ) 求点P、Q的坐标;
(Ⅱ) 若另有两点M(a,-a)、N(-a,a),记f(x)=![]() ·
·![]() .当点P在上半圆上运动时,求函数f(x)的最大值.
.当点P在上半圆上运动时,求函数f(x)的最大值.
 |
参考答案
1.D 2.D 3.D 4.B 5.B 6.A 7.A 8.D 9. A 10.D
11.5 12. 直角三角形 13.-1 14.0 15. -2 16. ②③
17.解:(Ⅰ)原式=![]()
(Ⅱ)原式=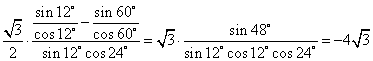
18.(Ⅰ)解![]() =(cosθ-3,sinθ),
=(cosθ-3,sinθ),![]() =(cosθ,sinθ-3),
=(cosθ,sinθ-3),
由已知:cos2θ-3 cosθ-3 sinθ+sin2θ=-1,sinθ+cosθ=![]() 得sin2θ=-
得sin2θ=-![]()
(Ⅱ)![]() =(cosθ+3,sinθ),(
=(cosθ+3,sinθ),(![]() )2=13,得cosθ=
)2=13,得cosθ=![]() ,θ=
,θ=![]()
设![]() 、
、![]() 夹角
夹角![]() ,则cos
,则cos![]() =
=![]() =sinθ=
=sinθ=![]() ,
,![]() =
=![]()
19.解(Ⅰ)化简得![]() ,由
,由![]() ,得a=1
,得a=1
(Ⅱ)由![]() ,所以单调减区间:
,所以单调减区间:![]()
对称中心:![]()
(Ⅲ)图略
 |
20.解:
(Ⅰ)设![]() a,
a,![]() b,
b,
由已知:![]()
![]() (a+ b)
(a+ b)
![]()
![]() (a+ b)
(a+ b)
![]() - a+
- a+![]() (a+ b)=-
(a+ b)=-![]() a+
a+![]() b
b
![]() - a+
- a+![]() b=
b=![]()
![]() ,所以C、N、M三点共线.
,所以C、N、M三点共线.
(Ⅱ)由已知,设![]() λ
λ![]()
![]() λ(a+ b)
λ(a+ b)
![]() - a+
- a+![]() (
(![]() λ-1)a+
λ-1)a+![]() λb,
λb,![]()
![]() 0,得λ=
0,得λ=![]() ,所以
,所以![]() =
=![]()
21.解(Ⅰ)P(cosx,sinx),Q(sinx ,cosx)
(Ⅱ)![]() =2 sinx cosx-2a(sinx -cosx)-2a2
=2 sinx cosx-2a(sinx -cosx)-2a2
设t=sinx -cosx=![]() ,x∈[0,π],则t∈[-1,
,x∈[0,π],则t∈[-1,![]() ]
]
则f(x)=-t2-2at-2a2+1,t∈[-1,![]() ]
]
①当-![]() ≤a≤1, fmax(x)=1-a2
≤a≤1, fmax(x)=1-a2
②当a>1, fmax(x)=2a-a2
③当a<-![]() , fmax(x)=-1-2
, fmax(x)=-1-2![]() a-2a2
a-2a2