数列解答题

1、有四个数，其中前三个数成等差数列，后三个数成等比数列，且第一个数与第四个数的和是16，第二个数与第三个数的和是12，求这四个数。

2、已知公差不为零的等差数列{a_n}与递增的等比数列{b_n}有如下关系：a₁=b₁=1，

a₃=b₃，a₇=b₅，求：(1){a_n}前n项之和S_n；(2){b_n}的通项公式。

3、等差数列{a_n}中，a₅=0.3，a₁₂=3.1，求a₁₈＋a₁₉＋a₂₀＋a₂₁＋a₂₂的值。

4、已知数列{a_n}的前n项和S_n,求通项公式a_n.：(1) S_n=10ⁿ－1;　(2)S_n=3ⁿ＋1.

5、已知数列{a_n}的前n项和公式.求证{a_n}是等差数列,并求出首项和公差.

6、设等差数列{a_n}的前n项和为S_n.已知a₃=12, S₁₂＞0,S₁₃＜0.(Ⅰ)求公差d的取值范围；(Ⅱ)指出S₁,S₂,…,S₁₂,中哪一个值最大,并说明理由.

7、已知等比数列{a_n}(a_n∈R)中,a₂=6,a₅=48,求它的前6项之和S_6.

8、在等差数列{a_n}中，已知a₁,a₄为x²－10x＋16=0的两根，并且a₄＞a₁，求前8项之和S₈的值。

9、已知等差数列{a_n}中，a₁＋a₄＋a₇=15，a₂·a₄·a₆=45，求数列{a_n}的通项公式。

10、等差数列{a_n}中, 其前10项和为100, 而前100项的和为10, 求前110项和.

11、某鱼塘养鱼,由于改进了饲养技术,预计第一年的增长率为200%,以后每年的增长率是前一年的一半,设原来的产量为a，由于存在池塘老化及环境污染等因素，估计每年将损失年产量的10%，照这样下去，以后每年的产量是否始终是逐年提高的？若是，请给予证明；若不是，请说明从第几年起，产量将不如上一年（参考数据lg2=0.3010,lg3=0.4771）

12、数列{a_n}既是等差数列又是等比数列。①求证该数列必是常数列；②若a_n+1=，求该数列前200项的和。

13、在等比数列{a_n}中，已知前10项和为5，前20项和为15，求前30项和。

14、数列前n项之和Sn=3ⁿ＋a（a为常数），a取何值时此数列成等比数列？

15、将自然数按下表排列：

　　1　 2　 5　 10  17　…

　　4　 3　 6 　11  18　…

　　9　 8　 7 　12  19　…

　　16　15  14　13　20  …　

　　25　24  23　22　21  …　

　　……

(1)第1列中第m个数是多少？ 第1行中第n个数是多少？(2)若m≥n，则第m行（自上而下）、第n列（自左而右）的数是多少？若m＜n呢？(3)99在上起第几行、左起第几列？翰林汇

答案提示

1、0，4，8，16或15，9，3，1　　2、(1)；(2)

3、求得d=0.4,a₁=-1.3，原式＝(a₁₈+a₂₂)+(a₁₉+a₂₁)+a₂₀=5(a₁+19d)=31.5.

4、解： (1)∵n=1时,a₁=S₁=9,n≥2时,a_n=S_n－S_n–1=(10ⁿ－1)－(10^n–1－1)=9·10^n-1,且当n=1时, 有a₁=S₁=9;∴a_n=9·10^n–1(n≥1).

(2) ∵n=1时,a₁=3¹＋1=4, n≥2时,a_n=S_n－S_n–1=(3ⁿ＋1)－(3^n–1＋1)=2·3^n–1,且当n=1时,a₁=2·3⁰=2S₁=4,∴a_n=.

5、证明： (1)a₁=S₁=, a_n=S_n－S_n–1=(4n－1) (n≥2),且当n=1时,a₁==S₁,

∴a_n=(4n－1) (nN).  ∵a_n+1－a_n=[4(n－1)－1]－(4n－1)=,

∴{a_n}是以为首项,为公差的等差数列.

6、解： (Ⅰ)依题意,有

，即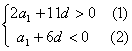

由a₃=12,得　a₁=12－2d　 (3)

将(3)式分别代入(1),(2)式,得　，∴.

(Ⅱ)由d＜0可知 a₁＞a₂＞a₃＞…＞a₁₂＞a₁₃.

因此,若在1≤n≤12中存在自然数n,使得a_n＞0,a_n+1＜0,

则S_n就是S₁,S₂,…,S₁₂中的最大值.

由于　S₁₂=6(a₆+a₇)＞0,　S₁₃=13a₇＜0，即 a₆+a₇＞0, a₇＜0.

由此得　a₆＞－a₇＞0.因为a₆＞0, a₇＜0,故在S₁,S₂,…,S₁₂中S₆的值最大.

7、解： 由通项公式得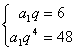，解得 q=2,　a₁=3，∴.

8、解：x²－10x＋16=0的两根为x₁=2，x₂=8，

由于a₄＞a₁且为两根，知a₄＝8，a₁＝2，由此得公差d=2，所以S₈＝4(2a₁＋7d)=72

9、a_n=2n-3或a_n=13-2n

10、解 由S₁₀=100, S₁₀₀=10　∴S₁₀₀－S₁₀=－90，即a₁₁+a₁₂+…+a₁₀₀=－90.

∴a₁₁+a₁₀₀=－2, 而a₁+a₁₁₀=a₁₁+a₁₀₀=－2，

∴.

11、从第六年起, 产量将不如上年。翰林汇

12、①答案：略；②1000.

13、解：记A＝a₁＋a₂＋…＋a₁₀,B=a₁₁＋a₁₂…＋a₂₀，　C＝a₂₁＋a₂₂＋…+a₃₀,

则A＝5，B＝S₂₀－S₁₀=10.A，B，C成等比，C＝

故S₃₀＝A＋B＋C＝35.

14、a=-1

15、(1)；(2)，若m＜n，为；

(3)解不等式(m－1)²＜99＜m²，得m=10，因此99在上起第10行，左起第2列。