洛阳市名校联考：2004—2005学年上学期月考试卷

高 一 数 学

一、 选择题(每小题5分，满分60分)　　

1.设集合u={1,2,3,4,5},A={1,2,3},B={2,5},则A ∩(C_uB)=

A. {2}　　　　　　　　　　 B. {2,3}　　　　　　　　　C. {3}　　　　　　　　　　D. {1,3}

2．不等式0<2x-1<5的解集为

A.{ x-2<x<3}　　　　　　　　　　　　　　　　　　　　 B. { x-2<x<2}

C. { xx<-2或x>3}　　　 　　　　　　　　　　　　D. { x-2<x<3且x≠}

3.三个数a=0.8^-1 , b=0.8,c=log_0.83,则a, b, c的大小关系是

A．a>b>c　 　　　　　 B. c>a>b　　　　　　　　　 C. b>a>c　 　　　　　　D. c>b>a

4.等差数列{a_n}的前n项和为S_n , 若a₃+a₁₇=10,则S₁₉的值

A．是55　 　　　　　　 B.是95　 　　　　　　　　 C.是100　 　　　　　　 D.不能确定

5．已知函数f(x)=lg,若f(a)=b,则f(-a)=　

A.b　 　　　　　　　　　 B.-b　　　　　　　　　　　 C. 　　　　　　　　 D.-

6.ax²+2x+1=0 至少有一个负的实根的充要条件是　

A.0<a≤1　 　　　　　　B. a<1　　　　　　　　　　　　C. a≤1　　　　　　　　　　D.0<a≤1或a<0

　　　　　　　　 a(a≤b)

7.定义运算a*b=　　　　 例如，1*2=1，则1*2^x的取值范围

　　　　　　　　 b(a>b)

A. (0,1)　　　　　　　　　　B.(-∞,1 　　　　　　　　　C. (0,1 　　　　　　　 D.  1,+∞)

8.已知集合M={ x-1≤x<2}, N={ xx-a<0}，若M∩N≠Ф，则a的范围为　

A. (-∞, 2 　　　　　　 B. (-1,+∞ )　　　　　　　　C. [-1, +∞)　　　　　　 D.[ -1, 1]

9. 若函数y=a^x+b-1(a>0且a≠1 )的图象经过一、三、四象限，则下列结论中正确的是

A. a>1且b<1　　 　 B. 0<a<1 且b<0　　　　 C. 0<a<1 且b>0　　　D. a>1 且b<0

10.设Sn=1-2+3-4+…+(-1)^n-1n,则S_4m+S_2m+1+S_2m+3(nN^*)的值是

A. 0　　　　　　　　　　 B. 3　　　 　　　　　　　 C.4　　　　　　　　　　　　　D. 随m的变化而变化

11.如果f(n+1)=f(n)+1(n=1,2,3,…) 且f(1)=2,则f(100)=

A. 99　　　　　　　　　 B. 100　　　　　　　　　　 C.101　　　　　　　　　　　D.102

12.函数y=log_ax在[2,+ ∞上恒有y>1,则实数a的取值范围是

A. (,1)∪(1,2)　　　 　　　　　　　　　　　　　　B. (0，)∪(1,2)　

C. (1,2)　　　　　　　　　　　　　　　　 　　　　　 D. (0，)∪(2,+ ∞)

二．填空题(每小题4分，满分16分)

13．函数y=log(x²-x)的递增区间为 　　　

14．函数y=+1(x≥1)的反函数为　　　　 　　　　　　　　　　　　　　　　　　　　　

15．若A是B的充分不必要条件，则A是B的　　　　　　　　

16．若lgx , lg(x-2y) , lgy成等差数列，则^log=　　　　

洛阳市名校联考：2004—2005学年上学期月考试卷

高一数学答题卷

题号	一	二	三						总分
			17	18	19	20	21	22
分数

请将选择题答案填入下表:

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

13．　　　　　　　　　　　　　　　 　　 14．　　　　　　　　　　　　　　　

15．　　　　　　  　　　　　　　　 　　 16．　　　　　　　　　　　　　　　

三．解答题（满分74分）(第17-21题每题12分，第22题14分，共74分)

17、等差数列{a_n}的前n项和记为Sn,已知a₁₀=30，a₂₀=50

(1)求通项a_n ;

(2)若Sn=242，求n .

18.比较log_x3x与log_x5的大小(x>0且x≠1)

得分	评卷人

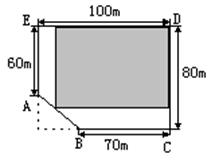
19.某房地产公司要在荒地ABCDE(如图)上划出一块长方形的地面修建一幢公寓楼，问如何设计才能使公寓楼地面的面积最大，并求出最大的面积。

得分	评卷人

20.已知函数f(x)=3^x+1+9^x-12的反函数是f^－1 (x)

(1) 求f^－1 (6) 的值;

(2)要使f^－1 (a)有意义，求a的取值范围.　　

得分	评卷人

21.已知数列{a_n}的前n 项和为Sn=32n-n²　

(1)求a_n的通项公式;

(2)若b_n= a_n ，求{b_n}的前n项和T_n。　　　　

22.设f(x)在定义域A上是单调递减函数，又F(x)=a^f(x) (a>0), 当f (x)>0时，F(x)>1

求证：(1)f(x)<0时，F(x)<1;

(2)F(x)在定义域A上是减函数.

数学试卷参考答案

一、选择题：

DDABB　　CCBDB　　CA

二、填空题：

13. （-∞,0）　　14.　y=x²-2x+2(x≥1)

15． 必要不充分条件　16.  4

三、解答题：

17.　解：（1）由a_n=a₁+(n-1)d， a₁₀=30,　a₂₀=50

得方程组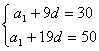： ……（3分）解得 a₁=12,d=2

所以，a_n=2n+10……（6分）

（2）由s_n=na₁+d,s_n=242得方程

12n+×2=242……（10分）

解得：n=11或n=-22（舍去）……（12分）

18．解：∵x>0且x≠1

当3x=5即x=时，log_x（3x）=log_x5……（2分）

当0<x<1时，3x<3<5　∴log_x（3x）>log_x5……（3分）

当1<x<时，3x<5　∴log_x（3x）<log_x5……（8分）

当x>时，3x>5　∴log_x（3x）>log_x5……（11分）

综上知：当x=时， log_x（3x）>log_x5

当0<x<1或x>时，log_x（3x）>log_x5

当1<x<时，log_x（3x）<log_x5……（12分）

19. 解：设长方形为DMNG（如图），且NG=xm(0<x<80)，矩形DMNG的面积为S（m²）……（1分）

延长EA、CB交于点P，延长GN交CH于点Q，则有Rt△APB∽Rt△BQN,所以

∴BQ=……（4分）

∴MN=CQ=BC+BQ=70+=-……（5分）

G

于是S=NG·MN=-……（8分）

Q

N

M

P

=-

∵

∴当x=时，S有最大值.……（11分）

答：只要使得与AE平行的长方形的一边长为m时，公寓楼的地面面积最大有最大值为m². ……（12分）

20． 解：（1）令3^x+1+9^x_12=6……（4分）　得x=1……（5分）

即f ^–1(6)=1……（6分）

(2)令 3^x+1+9^x-12=a, ……（9分）

]即a=，……（11分）

∴a(-12,+)时，f^-1(a)有意义. ……（12分）

21．解：……（1分）

　　　　n≥2时，a_n=s_n-s_n-1……（2分）

　　　　　　　　  =(32n-n²)-[32(n-1)-(n-1)²]

　　　　　　　　  =32-(2n-1)

　　　　　　　　  =-2n+33……（3分）

∴a_n=-2n+33(nN*)……（4分）

由a_n=-2n+33>0得n<

∵nN*，∴n=1,2,…，16时a_n>0

同理n=17，18，…，时，a_n<0……（6分）

∴1≤n≤16时

=a₁+a₂+…+a_n=32n-n²……（8分）

n≥17时

= a₁+a₂+…+a₁₆- a₁₇ -a₁₈-…-a_n

=-（a₁+a₂+…+a_n）+2s₁₆

=-（32-n²）+2（32×16-16²）

=n²-32n-512……（11分）

∴Tn=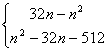　……（12分）

22.　证明：

（1）f(x)>0时，F(x)=a^f(x)>1,则f(x)<0时，

　　 -f(x)>0……（2分）

∴a^-f(x)>1　∴　 0<a^f(x)<1

∴F(x)<1……（4分）

(2)设x₁<x₂，x_1、x₂A……（5分）

∵f(x)在A上为减函数， ∴f(x₁)>f(x₂)

即f(x₂)-f(x₁)<0，而F（x₂）-F(x₁)=

a^f(x2)-a^f(x1)=a^f(x1)[a^f(x2)-f(x1)-1] ……（8分）

∵a>0,　 ∴a^f(x1)>0,且当f（x₂）-f(x₁)<0

而f（x）<0时，F（x）<1

∴a^f(x2)-f(x1)<1　　∴F(x₂)-F(x₁)<0

∴F（x₂）<F(x₁)

∴F(x)在定义域A上是减函数……（12分）