高一数学下末综合练习(一)
姓名 班级 得分
一、选择题 (本大题共12个小题,每小题5分,共60分)
1、 已知![]() ,则
,则![]() 的值为( )
的值为( )
(A)
-![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2、按向量![]() 把(2,
把(2,![]() )平移到(1,
)平移到(1,![]() ),则
),则![]() 把点(
把点(![]() ,2)平移到点 ( )
,2)平移到点 ( )
(A)(![]() ,1) (B)(
,1) (B)(![]() ,3) (C)(
,3) (C)(![]() ,3) (D)(
,3) (D)(![]() ,1)
,1)
3、已知![]() 等于 ( )
等于 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4、已知![]() 的图象 ( )
的图象 ( )
A.与g(x)的图象相同 B.与g(x) 图象关于y的轴对称
C.由g(x)的图象向左平移![]() 个单位得到 D.由g(x)的图象向右平移
个单位得到 D.由g(x)的图象向右平移![]() 个单位得到
个单位得到
5、在![]() 中,
中,![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、已知A(1,2),B(3,4),C(5,0)则△ABC一定是 ( )
(A)等腰直角三角形 (B)等边三角形 (C)等腰三角形 (D)直角三角形
7、已知![]() ,则
,则![]() 等于( )
等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D) ![]()
8、列不等式中,成立的是( )
(A)sin(-![]() )<sin(-
)<sin(-![]() ) (B)sin3>sin2
) (B)sin3>sin2
(C)cos(-![]() )<cos(-
)<cos(-![]() ) (D)cos
) (D)cos![]() <cos
<cos![]()
9、如果满足∠ABC=60°,AC=12,BC=k的△ABC恰有一个,那么k的取值范围是( )
A.k=8![]() B.0<k≤12 C.k≥12 D.0<k≤12或k=8
B.0<k≤12 C.k≥12 D.0<k≤12或k=8![]()
10、已知a=(1,2),b=(-3,2),向量ka+b与向量a-3b垂直, 向量ma+b与向量a-3b平行(k,m为实数),k+3m的值为
(A)17 (B)18 (C)19 (D)20
11、已知![]() ,若0≤θ≤π,使函数f(x)为偶函数的θ为
,若0≤θ≤π,使函数f(x)为偶函数的θ为
(A) ![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D)![]()
12、已知向量![]() ,
,![]() 且a、b夹角为
且a、b夹角为![]() ,则向量a+b与a-b的夹角是
,则向量a+b与a-b的夹角是
(A) ![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D)![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题 (本大题共四个小题,每小题5分,共20分)
13、把一个函数的图象按向量![]() =(3,
=(3,![]() )平移后得到图象的解析式为y=
)平移后得到图象的解析式为y=![]() ,则原来的函数解析式是_______________.
,则原来的函数解析式是_______________.
14、在![]() 中,角
中,角![]() 的对边长分别为
的对边长分别为![]() ,若
,若![]() ,且
,且![]() 成等差数列,求
成等差数列,求![]() 值等于
.
值等于
.
15、已知![]() =
.
=
.
16、设两向量![]() 满足
满足![]()
![]() 的夹角为60°,若向量2t
的夹角为60°,若向量2t![]() 与向量
与向量![]() 的夹角为钝角,则实数t的取值范围是
.
的夹角为钝角,则实数t的取值范围是
.
三、解答题 (本大题共6个小题,共70分)
17、已知△ABC的三个内角A、B、C满足:A+C=2B,![]() ,求
,求![]() 的值
的值
18、(本小题满分12分)设![]()
![]()
![]()
![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() 与
与![]() 的夹角为
的夹角为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
19、设![]() ,
,![]() ,
,
![]() 求证
求证![]() +
+![]() +
+![]() =0
=0
20、(本大题满分12分)设![]() 、
、![]() 是两个不共线的非零向量(t∈R)
①若
是两个不共线的非零向量(t∈R)
①若![]() 与
与![]() 起点相同,t为何值时,
起点相同,t为何值时,![]() ,t
,t![]() ,
,![]() (
(![]() +
+![]() )三向量的终点在一直线上?②若
)三向量的终点在一直线上?②若![]() =
=![]() 且
且![]() 与
与![]() 夹角为60°,那末t为何值时
夹角为60°,那末t为何值时![]() -t
-t![]() 的值最小?
的值最小?
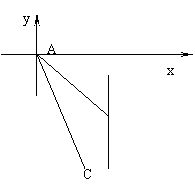 21、如图,甲船在A处,乙船在A处的南偏东
21、如图,甲船在A处,乙船在A处的南偏东![]() 方向,距A有9n mile,并以20 n mile/h的速度沿南偏西
方向,距A有9n mile,并以20 n mile/h的速度沿南偏西![]() 方向行驶,若甲船以28n mile/h的速度行驶,应沿什么方向,用多少h能尽快追上乙船?
方向行驶,若甲船以28n mile/h的速度行驶,应沿什么方向,用多少h能尽快追上乙船?
 |
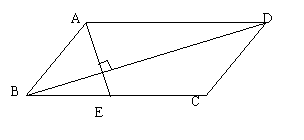 22、如图,在平行四边形ABCD中,BC=2AB,∠ABC=60°,自A向对角线BD引垂线,并延长交BC于E,求BE:EC
22、如图,在平行四边形ABCD中,BC=2AB,∠ABC=60°,自A向对角线BD引垂线,并延长交BC于E,求BE:EC
高一数学综合练习(一)(答案)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | D | C | A | A | C | C | D | B | A | C |
13,y=![]() ;14,
;14,![]() ;15,
;15,![]() ;16,
;16,![]() ;
;
17、解:∵A+C=2B,∴B=![]() ,∴A+C=
,∴A+C=![]() ,
,
由![]() 得
得![]() ,
,![]() ,令t=
,令t=![]() ,则有
,则有
![]() ,解得t=
,解得t=![]() ,或t=
,或t=![]() ,∵
,∵![]() ,
,
∴![]() =
=![]()
18、解:![]() ∴
∴![]()
![]() ∴
∴![]()
![]()
∴![]()
19、证明:![]() +
+![]() +
+![]() =
=
![]() ,而
,而
![]() =0,
=0,![]() =0
=0
∴![]() +
+![]() +
+![]() =0
=0
20、:①设![]() -t
-t![]() =m[
=m[![]() -
-![]() (
(![]() +
+![]() )](m∈R) 化简得
)](m∈R) 化简得![]()
![]() =
=![]()
![]()
∵![]() 与
与![]() 不共线 ∴
不共线 ∴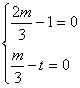
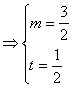
∴t=![]() 时,
时,![]() 、t
、t![]() 、
、![]() (
(![]() +
+![]() )终点在一直线上 ②
)终点在一直线上 ②![]() -t
-t![]() 2=(
2=(![]() -t
-t![]() )2=
)2=![]() 2+t2
2+t2![]() -2t,
-2t,
![]()
![]() cos 60°=(1+t2-t)
cos 60°=(1+t2-t)![]() 2, ∴t=
2, ∴t=![]() 时,
时,![]() -t
-t![]() 有最小值
有最小值![]()
21、解:设用t h,甲船追上乙船,且在C处相遇,那么在△ABC中,AC=28t,BC=20t,AB=9, ∠ABC=180°-15°-45°=120°,由余弦定理得:
(28t)2=81+(20t)2-2×9×20t×(![]() ),128t2-60t-27=0,t=
),128t2-60t-27=0,t=![]() ,(t=
,(t=![]() 舍去)
舍去)
AC=21(n mile),BC=15(n mile),根据正弦定理,得sinBAC=![]()
又∠ABC=120°,∴∠BAC为锐角,∠BAC=![]() ,而
,而![]()
甲船沿南偏东![]() 的方向用
的方向用![]() 小时可以追上乙船
小时可以追上乙船
22、解:设![]() ,
,![]() ,BE:EC=m:n,则
,BE:EC=m:n,则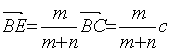
而![]() ,
,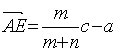 ,又
,又![]() ,且
,且![]() ⊥
⊥![]()
即(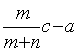 )(c+a)=0.而
)(c+a)=0.而![]() =
=![]() ,故
,故![]()
∴4m-n-(m+n)=0, ∴3m=2n,故 BE:EC=2:3