黄冈市蕲春一中高一数学同步单元测试（2）
第四章：三角函数 第二单元 和差倍半角公式测试题
命题人 黄冈蕲春一中 高级教师刘杰峰
一、选择题：
1．(05春北京)在△ABC中，已知2sinAcosB＝sinC，则△ABC一定是( )
A．直角三角形 B．等腰三角形 C．等腰直角三角形 D．正三角形
2．的值是( )
A． B． C． D．
3．f(x)＝的值域为( )
A．(――1,―1) ∪(―1, ―1) B．[,―1) ∪(―1, ]
C．(,) D．[,]
4．已知x∈(－,0)，cosx＝，则tan2x等于( )
A． B．－ C． D．－
5．(2004春北京)已知sin(θ＋π)＜0，cos(θ－π)＞0，则下列不等关系中必定成立的是( )
A．tan＜cot， B．tan＞cot， C．sin＜cos， D．sin＞cos．
6．(04江苏)已知0＜α＜，tan＋cos＝，则sin(α－)的值为( )
A． B． C． D．－
7．等式sinα＋cosα＝有意义，则m的取值范围是( )
A．(－1,) B．[－1,) C．[－1,] D．[―,―1]
8．在△ABC中，tanA tanB＞1是△ABC为锐角三角形的( )
A．充要条件 B．仅充分条件 C．仅必要条件 D．非充分非必要条件
9．已知α.β是锐角，sinα＝x，cosβ＝y，cos(α＋β)＝－，则y与x的函数关系式为( )
A．y＝―＋x (＜x＜1) B．y＝―＋x (0＜x＜1)
C．y＝――x (0＜x＜) D．y＝――x (0＜x＜1)
10．已知α∈(0,π)，且sinα＋cosα＝，则tanα的值为( )
A．－ B．－或－ C．－ D．或－
11．(05全国)在△ABC中，已知tan＝sinC，则以下四个命题中正确的是( )
(1)tanA·cotB＝1． (2)1＜sinA＋sinB≤．
(3)sin2A＋cos2B＝1． (4)cos2A＋cos2B＝sin2C．
A．①③ B．②④ C．①④ D．②③
12．函数y＝的值域为( )
A．[－,] B．[－,1] C．[－1, ] D．[－1,1]
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：
13．(03上海)若x＝是方程2cos(x＋α)＝1的解，α∈(0,2π)，则α＝＿＿＿＿＿＿．
14．已知cosθ＋cos2θ＝1，则sin2θ＋sin6θ＋sin8θ＝＿＿＿＿＿＿＿＿＿＿＿＿
15．函数y＝3sin(x＋20°)＋5sin(x＋80°)的最大值是＿＿＿＿＿＿＿＿＿
16．若圆内接四边形ABCD的四个顶点A、B、C、D把圆周分成∶∶∶＝4∶3∶8∶5，则四边形四个内角A、B、C、D的弧度数为＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
17．设cos(α－)＝－，sin(－β)＝，且＜α＜π，0＜β＜，求cos(α＋β)．
18．已知f(x)＝2asin2x－2asinx＋a＋b的定义域是[0, ]，值域是[－5,1]，求a、b的值．
19．(04湖北)已知6sin2α＋sinαcosα－2cos2α＝0，α∈[,π)，求sin(2α＋)的值．
20．(05北京)在△ABC中，sinA＋cosA＝，AC＝2，AB＝3，求tanA的值和△ABC的面积．
21．在矩形ABCD中，AB＝a，BC＝2a，在BC上取一点P，使得AB＋BP＝PD，求tan∠APD的值．
22．是否存在锐角α和β，使α＋2β＝①，且tantanβ＝2－②，同时成立？若存在，求出α和β的值；若不存在，请说明理由．
答案：
1．B 由2sinAcosB＝sin(A＋B)
sin(B－A)＝0B＝A．
2．C 原式＝＝＝．
3．B 令t＝sin x＋cos x＝sin(x＋)∈[―,―1)∪(―1, ]．
则f(x)＝＝∈[,―1)∪(―1, ]．
4．D
5．B ∵sinθ＞0，cosθ＜0，tan－cot＝－＝－＞0．
∴tan＞cot．
6．B tan＋cot＝＝．∴sinα＝．cosα＝．
sin(α－)＝sinα－cosα＝．
7．C8．A
9．A y＝cosβ＝cos[(α＋β)－α]＝cos(α＋β)cosα＋sin(α＋β)sinα
＝―＋x＞04x＞3＜x＜1．
10．A 解：当α∈(0, )时，sinα＋cosα＝sin(α＋)＞1．故α∈(,π)．
∴sinα＞0,cosα＜0．且sinα＞cosα∴tanα＞1．
由(sinα＋cosα)2＝sin2α＝－＝－．
tanα＝－或tanα＝－(舍)．
11．B 解：由tan＝＝＝sinC
∴cosC＝0，C＝．
∴A＋B＝．故①式＝tan2A≠1。②式＝sinA＋cosA＝sin(A＋)∈(1，]，
③式＝2sin2A≠1，④式＝cos2A＋sin2A＝1＝sin2C．
12．D 解：y＝sinx＋ycosx＝2ysin(x＋φ)＝≤1．
－1≤y≤1
13．
14．1 解：cosθ＝sin2θ，∴sin6θ＝cos3θ，sin8θ＝cos4θ．
∴sin2θ＋sin6θ＋sin8θ＝cosθ＋cos3θ＋cos4θ＝cosθ＋cos2θ(cosθ＋cos2θ)
＝cosθ＋cos2θ＝1．
15．7 解：y＝3sin(x＋20°)＋5[sin(x＋20°)cos60°＋cos(x＋20°)sin60°]
＝sin(x＋20°)＋cos(x＋20°)
＝7sin(x＋20°＋φ)≤7．
16．π, ,, 解：∵＝．故四条弧所对圆心角分别为，，，．
四内角分别为(＋)＝π．(＋)＝，，．
17．分析：∵＝(α―)―(－β)．
解：∵α∈(,π)β∈(0, )．
∴＜α－＜π，－＜－β＜．
∴由cos(α－)＝－得sin(α－)＝，
由sin(－β)＝．得cos(－β)＝．
∴cos＝cos[(α―)―(―β)]＝…＝．
∴cos(α＋β)＝2×()2－1＝－．
18．解：令sinx＝t，∵x∈[0, ]．∴t∈[0,1]．
f(x)＝g(t)＝2at2－2at＋a＋b＝2a(t－)2＋b．
当a＞0时，则
当a＜0时，则．
19．解：依题知α≠，cosα≠0．
方程可化为6tan2α＋tanα－2＝0．tanα＝－或 (舍)．
∴sin(2α＋)＝sin2αcos＋cos2α·sin
＝sinαcosα＋(cos2α－sin2α)＝＋·
＝＋×＝－＋．
20．解：sinA＋cosA＝cos(A－45°)＝，
∴cos(A－45°)＝．
∵0°＜A＜180°，
∴A－45°＝60°，A＝105°，
∴tanA＝tan(60°＋45°)＝―2―，
sinA＝sin(60°＋45°)＝，
∴S△ABC＝AC·AB．sinA＝×2×3×＝(＋)．
21．解：如图作PE⊥AD于E．设BP＝X．
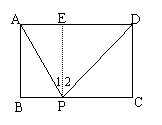则x＋a＝，
∴x＝，
∴AE＝BP＝，DE＝PC＝a，
∴tan∠APD＝tan(∠1＋∠2)＝＝18．
22．解1：由①得＋β＝，
∴tan(＋β)＝＝．
将②代入得tan＋tanβ＝3－．
∴tan,tanβ是方程x2―(3―)x＋2－＝0的两根．
解得x1＝1，x2＝2－．
若tan＝1，则α＝与α为锐角矛盾．
∴tanβ＝1, tan＝2－，
∴β＝．代入①得α＝．满足tan＝2－．
解2：由①得＝－β，代入②得：
tan(－β)·tanβ＝2－·tanβ＝2－．
tan2β―(3―)tanβ＋2－＝0；tanβ＝1或2－．
若tanβ＝1，则β＝，α＝．
若tanβ＝2－．代入②得cot＝1，则α＝不合题意．
故存在α＝，β＝使①、②同时成立．