北京英才苑学科专家组 安振平 审定
2003－2004学年度下学期
高中学生学科素质训练
高 一 数 学 期 末 测 试 题
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
（满分150，时间120分钟）
|
一、选择题（每小题5分，共60分，请将所选答案填在括号内）
1．在△ABC中，D、E、F分别是BC、CA、AB的中点，点M是△ABC的重心，则
等于 （ ）
A．
B．4
C．
D．
2．在△ABC中，若
则△ABC是 （ ）
A．等腰三角形 B．直角三角形 C．等边三角形 D．等腰直角三角形
3．在△ABC中，已知
，则
的值是 （ ）
A．
B．
C．
D．
4．已知
C为
上距A较近的一个三等分点，D为
上距C较近的一个三等分点，用
表示
的表达式为 （ ）
A．
B．
C．
D．
5．若
，则
的值为 （ ）
A．
B．－ C． D．－
6．函数
的值域为 （ ）
A．[－1，1] B．[0，1] C．[－
，2] D．[，2]
7．
、
是锐角三角形的两个内角，则有 （ ）
A．
B．
C．
D．
8．函数
在
上的反函数为 （ ）
A．
B．
C．
D．
9．
是
的 （ ）
A．充要条件 B．必要不充分条件
C．充分不必要条件 D．既不充分也不必要条件
10．关于
的方程
内有相异两实根，则
的取值范围为
（ ）
A．（－3，1） B．（0，1） C．（－2，1） D．（0，2）
11．已知
，则函数
的值域为 （ ）
A．[0，2] B．[－1，3] C．[－1，2] D．[0，3]
12．已知
、
是夹角为60°的两个单位向量，则
=2+与
=2－3的夹角的余弦是 （ ）
A． B．－ C．
D．－
|
二、填空题（每小题4分，共16分，请将答案填在横线上）
13．已知
且
则
=
.
14．函数
的定义域为
.
15．已知奇函数
满足
，且当
时，
则
的值为
.
16．在△ABC中，A（－1，1），B（3，1），C（2，5），角A的内角平分线交对边于D，则向量
的坐标等于
.
三、解答题（本大题共74分，17—21题每题12分，22题14分）
|
17．已知
求证：
.
|
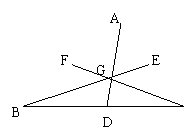
18．设G是△ABC内一点，延长AG、BG、CD交BC、AC、AB于点D、E、F，且
求证：
|
19．在△ABC中，
满足
（1）试判断△ABC的形状；
（2）当
时，求
的值.
|
|
|
21．在△ABC中，A、B、C所对的边分别为a、b、c，且a、b、c成等比数列，求
的范围.
|
22．用向量的方法求下式的值：
高一下学期期末测试题数学参考答案
一、1．C 2．A 3．A 4．A 5．B 6．D 7．B 8．B 9．C 10．B 11．B 12．B
二、13．
14．
15．
16．（
）
三、 17．左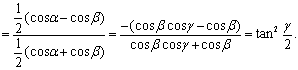
18． 如图存在
①
②
③
又
④
|
，
故
．
同理
，
． 又
， 故
． ⑤
由③、⑤及
共线 ， 且
为基底，
故
， 故
.
19．（1）△ABC为等腰三角形或直角三角形；
（2）当
时，
； 当C=90°时，
.
20．设
，
当
时，
有最大值
.
21．
． 令
，
22．构造一个正七边形. 
∴原式=