2006年度高一第二学期回校日数学考试问卷
一、选择题:每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内。
1.已知集合![]() ,
,![]() ,则
,则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知![]() 在映射
在映射![]() 下的象是
下的象是![]() ,则
,则![]() 在
在![]() 下的原象是 ( )
下的原象是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知![]() 是等差数列,五个数列①
是等差数列,五个数列①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]()
中仍是等差数列的个数是 ( )
A.1个 B.2个 C.3个 D.4个
4.已知![]() ,那么
,那么![]() 用
用![]() 表示是 ( )
表示是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知公差不为零的等差数列的第4、7、16项分别是某等比数列的第4、6、8项,则该等比数列的公比为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知函数![]() 是定义在[a,b]上的减函数,那么
是定义在[a,b]上的减函数,那么![]() 是 ( )
是 ( )
A.在![]() 上的增函数 B.在
上的增函数 B.在![]() 上的增函数
上的增函数
C.在![]() 上的减函数 D.在
上的减函数 D.在![]() 上的减函数
上的减函数
7.下列“![]() 或
或![]() ”形式的复合命题为假命题的是 ( )
”形式的复合命题为假命题的是 ( )
A.![]() :2为质数 q:1为质数
:2为质数 q:1为质数
B.![]() :
:![]() 为无理数
为无理数 ![]() :
:![]() 为无理数
为无理数
C.![]() :奇数集为
:奇数集为![]()
![]() :偶数集为
:偶数集为![]()
D.![]() :
:![]()
![]() :
: ![]()
8.已知条件甲:![]() ;乙:
;乙:![]() ,那么条件甲是条件乙的 ( )
,那么条件甲是条件乙的 ( )
A.充分且必要条件 B.充分不必要条件
C.必要不充分条件 D.不充分也不必要条件
|
10.数列
![]() 是由正数组成的等比数列, 且公比不为1,则
是由正数组成的等比数列, 且公比不为1,则![]() 与
与![]() 的大小关系为 ( )
的大小关系为 ( )
A.![]() >
>![]() B.
B.![]() <
<![]()
C.![]() =
=![]() D.与公比的值有关
D.与公比的值有关
11.设![]() 是由正数组成的等比数列,公比
是由正数组成的等比数列,公比![]() ,且
,且![]() ,则
,则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.当x∈[0,2]时,函数f(x)=ax2+4(a-1)x-3在x=2时取得最大值,则a的取值范围是
A.[-![]() ,+∞) B.[0,+∞) C.[1, +∞) D.[
,+∞) B.[0,+∞) C.[1, +∞) D.[![]() ,+∞)
,+∞)
二、填空题:每小题4分,共16分.请把答案填在题中横线上.
13.不等式![]() 的解集为
的解集为![]() ,那么
,那么![]() 的值等于___________。
的值等于___________。
14.定义符号函数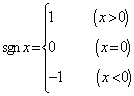 , 则不等式:
, 则不等式:![]() 的解集是 ;
的解集是 ;
15.老师在黑板上按顺序写了4个数构成一个数列,四个同学各指出这个数列的一个特征:
张三说:前3项成等差数列;李四说:后3项成等比数列;
王五说:4个数的和是24;马六说:4个数的积为24;
如果其中恰有三人说的正确,请写出一个这样的数列 ;
16.把下面不完整的命题补充完整,并使之成为真命题:
若函数![]() 的图象与
的图象与![]() 的图象关于
对称,则函数
的图象关于
对称,则函数![]() =
=
。
(注:填上你认为可以成为真命题的一件情形即可,不必考虑所有可能的情形).
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(本题满分12分)
已知集合![]() ,
,![]() ,
,![]() .若
.若![]() ,试确定实数
,试确定实数![]() 的取值范围.
的取值范围.
18.(本题满分12分)
在公差不为0的等差数列![]() 和等比数列
和等比数列![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ;(1)求
;(1)求![]() 的公差
的公差![]() 和
和![]() 的公比
的公比![]() ;
;
(2)设![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() 及前
及前![]() 项和
项和![]() .
.
19.(本题满分12分)
某渔场原有鱼2万斤,所养鱼的重量第一年的增长率为200%,以后每年的增长率都是前一年的一半,问:
1)饲养三年后的鱼的重量是多少;
2)如果因为环境污染,每年损失重量10%,那么经过多少年后鱼的重量开始减少。
20.(本题满分12分)
设数列{an}的前n项和为Sn,若对于任意的n∈N*,都有Sn=2 an-3n .
(1)求数列{an}的首项a1与递推关系式:an+1= f(an);
(2)先阅读下面定理:“若数列{an}有递推关系an+1=A an+B,其中A、B为常数,且
A≠1,B≠0,则数列![]() 是以A为公比的等比数列.”请你在第(1)题的基础上应用本定理,求数列{an}的通项公式;
是以A为公比的等比数列.”请你在第(1)题的基础上应用本定理,求数列{an}的通项公式;
(3)求数列{an}的前n项和Sn .
21.(本题满分12分)
已知![]() 满足
满足![]() ,求
,求![]() 的最大值与最小值及相应的
的最大值与最小值及相应的![]() 的值.
的值.
22(本题满分14)
(本题满分14分) 对于函数![]() ,若存在
,若存在![]() 成立,则称
成立,则称![]() 的不动点.如果函数
的不动点.如果函数![]() 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且![]() 。
。
(1)求函数![]() 的解析式;
的解析式;
(2)已知各项不为零的数列![]() ,求数列通项
,求数列通项![]() ;
;
(3)如果数列![]() 满足
满足![]() ,求证:当
,求证:当![]() 时,恒有
时,恒有![]() 成立.
成立.
2006年度高一第二学期回校日数学考试参考答案
一、选择题:(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | A | B | A | C | D | C | C | A | A | B | D |
二、填空题:(每小题4分,共16分)
13、![]() ; 14、
; 14、![]() ; 15、6,6,6,6或
; 15、6,6,6,6或![]() 2,2,6,18等;
2,2,6,18等;
16.如 ①x轴,-3-log2x ②y轴,3+log2(-x)
③原点,-3-log2(x) ④直线y=x, 2x-3
三、解答题:
17、(满分12分)
解:由题易得![]() ------2分
------2分 ![]() --------4分
--------4分
![]() --------6分
--------6分 ![]() ---8分
---8分
∵![]() ,∴
,∴![]() 且
且![]()
∴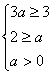 ,解得
,解得![]() --11分
∴
--11分
∴![]() 的取值范围是
的取值范围是![]() -----12分
-----12分
18、(本题满分12分)
解:(1)由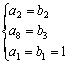 得
得![]() -----------3分
-----------3分
∴![]() ,即,
,即,![]()
又∵![]() ,∴
,∴![]() ,从而
,从而![]() ---------------6分
---------------6分
(2)∵![]() ,
,![]()
∴![]()
=![]() -------9分 从而,
-------9分 从而,![]()
=![]() ----------12分
----------12分
19.(Ⅰ)由题意:a1=2+2×2=6,a2=2+2×2+(2+2×2)=12,∵ a2=a1+a1×1,a3=a2+a2×![]() =12+6=18
=12+6=18
![]() ∴饲养3年后鱼的重量为8万斤。
∴饲养3年后鱼的重量为8万斤。
(Ⅱ)同理:a4=a3+a3 ×![]() ,a5=a4+a4×
,a5=a4+a4×![]() ,…
,…
∴ an=an-1+an-1![]() =an-1(1+
=an-1(1+![]() )
)
设第n年鱼的重量最大,则有
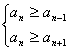 即
即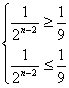
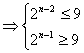
![]() ∴n=5 ∴从第6年(5年后)鱼的重量开始减少。
∴n=5 ∴从第6年(5年后)鱼的重量开始减少。
20、(本题满分12分)
解:(1)令n=1,S1=2a1-3. ∴a1 =3 又Sn+1=2an+1-3(n+1), Sn=2an-3n,
两式相减得,an+1 =2an+1-2an-3,-------3分 则an+1 =2an+3 --------4分
(2)按照定理:A=2,B=3,
∴{ an+3}是公比为2的等比数列.
则an+3=(a1+3)·2n-1=6·2n-1, ∴an =6·2n-1-3 . -------8分
(3)![]() ----------12分
----------12分
21、(本题满分12分)
解: 由题意可得![]() ,∴
,∴![]() --------------------------4分
--------------------------4分
又∵![]() =
=![]()
=![]() =
=![]() ----------------------------------------6分
----------------------------------------6分
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ------------------10分
------------------10分
即,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() --------------------12分
--------------------12分
22、(本题满分14分)
解:设![]() 得:
得:![]() 由违达定理得:
由违达定理得: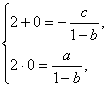
解得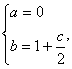 代入表达式
代入表达式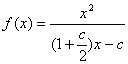 ,由
,由![]()
得![]() 不止有两个不动点,
不止有两个不动点,
![]() ………………………………………5分
………………………………………5分
(2)由题设得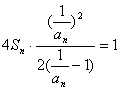 得
得![]() (A)
(A)
且![]() (B)
(B)
由(A)![]() (B)得:
(B)得:![]()
![]()
解得![]() (舍去)或
(舍去)或![]() ;由
;由![]() ,若
,若![]() 这与
这与![]() 矛盾,
矛盾,
![]() ,即{
,即{![]() 是以
是以![]() 1为首项,
1为首项,![]() 1为公差的等差数列,
1为公差的等差数列,
![]() ; ………………………………………………………………10分
; ………………………………………………………………10分
(3)证法(一):运用反证法,假设![]() 则由(1)知
则由(1)知![]()
![]()
∴![]() ,而当
,而当![]()
这与假设矛盾,故假设不成立,∴![]() .………………………………………14分
.………………………………………14分
证法(二):由![]()
得![]() <0或
<0或![]() 结论成立;
结论成立;
若![]()
![]() ,此时
,此时![]() 从而
从而![]()
即数列{![]() }在
}在![]() 时单调递减,由
时单调递减,由![]() ,可知
,可知![]() 上成立…14分
上成立…14分