苏州市第五中学2005～2006学年第二学期期中考试

高一数学试卷(苏教版)

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共100分，时间120分钟.

　 第Ⅰ卷（选择题，共60分）

一、选择题：本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 不等式的解集是　　　　　　　　　　　　　　　　　　　　　　  (　 )

A.　　 B.　　 C.　　  D.

2.在中，，，，则等于　　　　　　　　　　　　　　　 （　 ）

A.　　　　  B.或　　　　  C.或　　　　 D.

3.在等比数列中，，，则的前4项和为　　　　　　　　　  （　 ）

A.81　　　　　　　　  B.120　　　　　　　　　 C.192　　　　　　　　　  D.360

4.在中，若，，则　　　　　　　　　　　  (　 )

A.2　　　　　　　　　  B.　　　　　　　　　  C.　　　　　　  D.

5.有下列命题：

①棱锥的侧面只能是三角形；②棱柱的底面一定是正方形；

③棱台的侧棱延长后必交于一点；④棱柱的每个面都不可能是三角形.

其中，正确命题的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　  （　 ）

A.1　　　　　　　  B.2　　　　　　　　 C.3　　　　　　　　　 D.4

6.已知集合，，则　　　　　　　　  (　 )

A.　　 B.　　 C.　　  D.

7.设是等比数列，有下列四个命题：

①是等比数列；②是等比数列；③是等比数列；④是等比数列.

其中，正确命题的个数是　　　　　　　　　　　　　　　　　　　　　　　　　　  (　 )

A.1　　　　　　  B.2　　　　  C.3　　　　 D.4

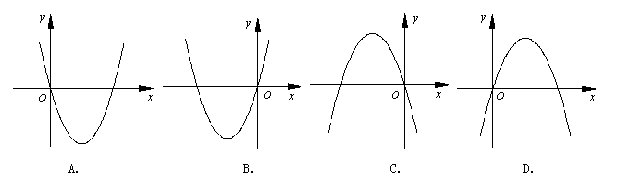8.等差数列中，，公差，为其前项和，对任意正整数，若点在以下四条曲线中的某一条上，则这条曲线应是　　　　　　　　　　　　　　　　　　　　 　(　 )

9.不等式的解集为 ，则实数与的和为　　　　　　　　　 (　 )

A.10　　　　  B.-10　　　　  C.14　　　　 D.-14

10.下列函数中，最小值是4的是　　　　　　　　　　　　　　　　　　  　　　　　( 　)

　　 A.　　 B. 　 C.　　 D.

11.等差数列中，公差，，则　　　　　　  (　 )

　　 A.40　　　　　　　　 B.45　　　　　 　 C.50　　　　　　 　 D.55

12.已知的面积为，则角等于　　　　　　　　　　　　　　　 （　 ）

A.　　　　　　　 B.　　　　　　　 C.　　　　　　 D.

第Ⅱ卷(非选择题 共90分)

二、填空题：本大题共6小题，每小题3分，共18分．把答案填在题中横线上．

13.在中，，，，那么　　　　 .

14.函数的值域是　　　　  .

15.在正项等比数列中，若，则　　 .

16.若对任意实数，不等式恒成立，则的取值范围是　　　 .

17.已知的三条边长成等比数列，对应的内角成等差数列，则的形状是　　　　　　　  .

18. 从20个连续正整数1，2，…，20中除去一个数，余下的19个数的算术平均数等于，则除去的那个数是　　　　　　 .

三、解答题：本大题共5小题，共46分．解答应写出文字说明，证明过程或演算步骤．

19.等差数列的前项和记为，已知，.

（Ⅰ）求通项；（Ⅱ）若，求.

　　

20.设，求证：.

21.三个正数成等差数列，且，又成等比数列，求的值.

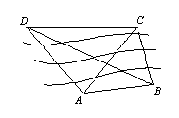
22.如图，为了测量河对岸两个建筑物之间的距离，在河岸这边取两点，测得，，，，又千米，在同一平面内，试求之间的距离.

23.正三角形的边长是2，分别在边上运动，且线段将的面积二等分，求线段长的取值范围.

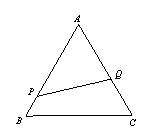
苏州市第五中学2005～2006学年第二学期期中考试

高一数学试卷参考答案(苏教版)

一、选择题

1～12. BBBAB　CCDDC　BD

二、填空题

13..　 14..　 15.16.　16..　 17. 等边三角形.　18.12.

三、解答题

19.（Ⅰ）由，得方程组

　　　

解得，所以　.

（Ⅱ）由得方程

　　　.

解得.　　

20.课本习题（解答见教参）

21.∵成等差数列，且，∴，.

设公差为，则，.

又∵成等比数列，∴，

即 ，　∴ ，

解得　 ，或.

当时，，，；

当时，，，.

∴的值分别为，或.

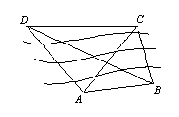22.由题意，得

　　　 ，

.

在中，，

∴.

在中，，，

∴为等腰三角形，∴.

在中，由余弦定理，得

　　　　　　　 

　　　　　　　　　 

　　　　　　　　　  .

∴千米.

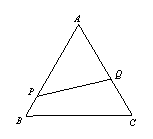23. 解答：设，().

∴ ，.

由余弦定理，得

  ，

∴ .

由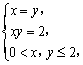解得.

故当时，.

又∵，∴，令，∵，∴，∴.

因此().

∵ 在上递减，在上递增，

∴ 当，或4时，取得最大值3，从而取得最大值.

故长的取值范围是.