北京英才苑学科专家组 安振平 审定
2003－2004学年度下学期
高中学生学科素质训练
高一数学同步测试（12）
正弦定理、余弦定理、解斜三角形
一、选择题（每小题5分，共60分，请将所选答案填在括号内）
1．在△ABC中，
，那么△ABC一定是 （ ）
A．锐角三角形 B．直角三角形
C．等腰三角形 D．等腰三角形或直角三角形
2．在△ABC中，
，则S△ABC= （ ）
A．
B．
C．
D．1
3．若
则△ABC为 （ ）
A．等边三角形 B．等腰三角形
C．有一个内角为30°的直角三角形 D．有一个内角为30°的等腰三角形
4．边长为5、7、8的三角形的最大角与最小角之和的 （ ）
A．90° B．120° C．135° D．150°
5．设A是△ABC中的最小角，且
，则实数a的取值范围是 （ ）
A．a≥3 B．a＞－1 C．－1＜a≤3 D．a＞0
6．△ABC中，∠A，∠B的对边分别为a,b，且∠A=60°，
，那么满足条件
的△ABC （ ）
A．有一个解 B．有两个解 C．无解 D．不能确定
7．已知△ABC的周长为9，且
，则cosC的值为 （ ）
A．
B． C．
D．
8．锐角△ABC中，
，则 （ ）
A．Q>R>P B．P>Q>R C．R>Q>P D．Q>P>R
9．△ABC的内角A满足
则A的取值范围是（ ）
A．（0，
） B．（，
） C．（，
） D．（，）
10．关于x的方程
有一个根为1，则△ABC一定是（ ）
A．等腰三角形 B．直角三角形 C．锐角三角形 D．钝角三角形
11．在△ABC中，
，则三角形最小的内角是（ ）
A．60° B．45° C．30° D．以上都错
12．有一长为1公里的斜坡，它的倾斜角为20°，现要将倾斜角改为10°，则坡底要伸长
（ ）
A．1公里 B．sin10°公里 C．cos10°公里 D．cos20°公里
二、填空题（每小题4分，共16分，答案填在横线上）
13．在△ABC中，a+c=2b，A－C=60°，则sinB= .
14．在△ABC中，已知AB=l，∠C=50°，当∠B= 时，BC的长取得最大值.
15．在△ABC中，已知AB=4，AC=7，BC边的中线
，那么BC=
.
16．△ABC的三个角A<B<C，且成等差数列，最大边为最小边的2倍，则三内角之比为
.
三、解答题（本大题共74分，17—21题每题12分，22题14分）
17．在△ABC中，a、b、c分别是角A、B、C的对边，设a+c=2b，A－C=
，求sinB的值.
18．设三角形各角的余切成等差数列，求证：相应各边的平方也成等差数列.
19．在△ABC中，BC=a，AC=b，AB=c，且
，试判断△ABC的形状.
20．设△ABC的三边长分别为a、b、c，求证：
.
21．已知A、B、C成等差数列，求
的值.
22．在奥运会垒球比赛前，C国教练布置战术时，要求击球手以与连结本垒及游击手的直线成15°方向把球击出，根据经验，通常情况下，球速为游击手最大跑速的4倍，问按这样布置，游击手能否接着球？
参考答案（12）
一、1.D 2.C 3.B 4.B 5.A 6.C 7.A 8.A 9.C 10.A 11.B 12.A
二、13．
14．40° 15．9 16．1:2:3
三、17．∵
， ∴
，
故
， ∴
．
18．∵
故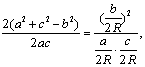
∴a2+b2=2b2 ，故得证．
19．△ABC是等腰三角形或直角三角形
20．
．
21．∵A+B+C=π， A+C=2B ， ∴A+C=
， 
，
，
故有
．
|
22．如图：设接球点为B，O为守垒，A为游击手出发点
，
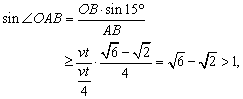
故不能接着球．