高中同步测控优化训练(十二)

第三章　数列(一)(B卷)

说明：本试卷分为第Ⅰ、Ⅱ卷两部分，共100分，考试时间90分钟.

第Ⅰ卷(选择题　共30分)

一、选择题(本大题共10小题，每小题3分，共30分)

1.设数列{a_n}、{b_n}都是等差数列，且a₁=25,b₁=75,a₂+b₂=100,那么由a_n+b_n所组成的数列的第37项为

A.0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.37

C.100　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.－37

解析：∵{a_n}、{b_n}为等差数列，∴{a_n+b_n}也为等差数列.设c_n=a_n+b_n,则c₁=a₁+b₁=100,而c₂=a₂+b₂=100,故d=c₂－c₁=0.∴c₃₇=100.

答案：C

2.设{a_n}为等差数列，则下列数列中，成等差数列的个数为

①{a_n²}　②{pa_n}　③{pa_n+q}　④{na_n}(p、q为非零常数)

A.1　　　　　　　　　　　　　　　B.2　　　　　　　　　　　　　　　C.3　　　　　　　　　　　　　　　D.4

解析：{pa_n}、{pa_n+q}的公差为pd(设{a_n}公差为d),而{na_n}、{a_n²}不符合等差数列定义.

答案：B

3.在等差数列{a_n}中，a₁>0,且3a₈=5a₁₃,则S_n中最大的是

A.S₂₁ B.S₂₀C.S₁₁ D.S₁₀

解析：3a₈=5a₁₃d=－a₁<0.a_n≥0n≤20.

答案：B

4.在{a_n}中，a₁=15,3a_n+1=3a_n－2(n∈N^*),则该数列中相邻两项的乘积为负数的项是

A.a₂₁和a₂₂ B.a₂₂和a₂₃

C.a₂₃和a₂₄ D.a₂₄和a₂₅

解析：a_n+1－a_n=,∴a_n=15+(n－1)(－)=.a_n+1a_n<0(45－2n)(47－2n)<0<n<.

∴n=23.

答案：C

5.数列{a_n}的通项公式为a_n=4n－1,令b_n=,则数列{b_n}的前n项和为

A.n²B.n(n+2)

C.n(n+1)　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.n(2n+1)

解析：∵a_n=4n－1,∴数列{a_n}是等差数列，且a₁=4－1=3.

∴b_n==2n+1.

显然数列{b_n}是等差数列，且b₁=2+1=3,

它的前n项和S_n=b₁+b₂+…+b_n==n(n+2).

答案：B

6.数列{a_n}中，a₁=1,a₂=,且n≥2时，有=,则

A.a_n=()ⁿB.a_n=()^n－1

C.a_n=　　　　　　　　　　　　　　　　　　　　　　　　　　D.a_n=

解析：∵,n≥2,

∴数列{}是等差数列.

∵a₁=1,a₂=,

∴首项=1,公差d=.

∴.∴a_n=.

答案：D

7.若{a_n}是等差数列，首项a₁>0,a₂₀₀₃+a₂₀₀₄>0,a₂₀₀₃·a₂₀₀₄<0,则使前n项和S_n>0成立的最大自然数n是

A.4005　　　　　　　　　　　　 B.4006　　　　　　　　　　　　 C.4007　　　　　　　　　　　　 D.4008

解析：∵a₁>0,a₂₀₀₃+a₂₀₀₄>0,a₂₀₀₃·a₂₀₀₄<0,

∴a₂₀₀₃>0,a₂₀₀₄<0.

S₄₀₀₆=×4006>0,

S₄₀₀₇=×4007=4007×a₂₀₀₄<0.

∴使前n项和S_n>0成立的最大自然数n是4006.故选B.

答案：B

8.已知数列｛a_n｝的通项公式为a_n=(－1) ^n－1·(4n－3),则它的前100项之和为

A.200　　　　　　　　　　　　　 B.－200　　　　　　　　　　　 C.400　　　　　　　　　　　　　 D.－400

解析：S₁₀₀=a₁+a₂+…+a₁₀₀

=1－5+9－13+17－…+(4×99－1)－(4×100－1)

=(1－5)+(9－13)+…+［(4×99－1)－(4×100－1)］

=－4×50=－200.

答案：B

9.数列｛a_n｝的前n项和S_n=3n－2n²(n∈N^*)，则当n≥2时，下列不等式中成立的是

A.S_n＞na₁＞na_n B.S_n＞na_n＞na₁

C.na₁＞S_n＞na_n D.na_n＞S_n＞na₁

解析：由S_n=3n－2n²可求得a_n=－4n+5,

∴a₁＞a_n(n≥2).

S_n=a₁+a₂+…+a_n＜na₁,

S_n=a₁+a₂+…+a_n＞na_n,

∴na_n＜S_n＜na₁.

答案：C

10.依市场调查结果预测某种家用商品以年初开始的n个月内累积的需求量为S_n(万件),近似地满足S_n=(21n－n²－5)(n=1,2,…,12),则按此预测在本年度内，需求量超过1.5万件的月份是

A.5月、6月　　　　　　　　　　　　　　　　　　　　　　　　　 B.6月、7月

C.7月、8月　　　　　　　　　　　　　　　　　　　　　　　　　 D.8月、9月

解析：第n个月需求量a_n=S_n－S_n－1=(－n²+15n+9),a_n>1.5，得(－n²+15n+9)>1.5.

解得6<n<9.∴n=7或8.

答案：C

第Ⅱ卷(非选择题　共70分)

二、填空题(本大题共4小题，每小题4分，共16分)

11.等差数列{a_n}中，a₁=－5,它的前11项的平均值是5，若从中抽取1项后余下的10项的平均值仍为5，则抽取的是第_______项.

解析：由－5×11+d=55,得d=2.由a_n=5,a_n=a₁+(n－1)d得n=6.

答案：6

12.在等差数列{a_n}中，若a₁+3a₈+a₁₅=120,则2a₉－a₁₀=________.

解析：∵{a_n}是等差数列，

∴a₁+3a₈+a₁₅=5a₈=120,即a₈=24.

又∵{a_n}是等差数列，∴a₈+a₁₀=2a₉.

∴2a₉－a₁₀=a₈=24.

答案：24

13.若△ABC三边a,b,c成等差数列，并且a²,b²,c²也成等差数列，则a,b,c的大小关系为_________.

①②

解析：由题意得

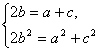
由①得c=2b－a,代入②整理得a²－2ab+b²=0.

∴a=b.

答案：a=b=c

14.已知a₁=－,a_n=a_n－1+(n∈N^*,n≥2),则a_n=_________.

解析：a_n=a_n－1+,

a_n－1=a_n－2+,

a_n－2=a_n－3+,

……

a₂=a₁+.

相加得a_n=a₁+

=－［()+()+…+()］

=－.

答案：－

三、解答题(本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤)

15.(本小题满分8分)在等差数列{a_n}中，a₁=－60,a₁₇=－12.

(1)求通项a_n;

(2)求此数列前30项的绝对值的和.

解：(1)a₁₇=a₁+16d,即－12=－60+16d,∴d=3.

∴a_n=－60+3(n－1)=3n－63.

(2)由a_n≤0,则3n－63≤0n≤21.∴a₁+a₂+…+a₃₀=－(a₁+a₂+…+a₂₁)+(a₂₂+a₂₃+…+a₃₀)=(3+6+9+…+60)+(3+6+…+27)=×20+×9=765.

16.(本小题满分10分)已知一元二次方程a(b－c)x²+b(c－a)x+c(a－b)=0有两个相等的实根，求证：，，成等差数列.

证明：∵二次方程有等根,

∴Δ=b²(c－a)²－4ac(b－c)(a－b)=0.

∴b²c²+a²b²+(2ac)²－4a²bc－4abc²+2ab²c=0.

∴(ab+bc－2ac)²=0.

∴ab+bc－2ac=0.

∴b(a+c)=2ac.

∴=+.

∴,,成等差数列.

注：本题也可这样做：∵x=1是方程的根，

∴x₁=x₂=1.

∴x₁x₂==1.

∴2ac=ab+bc.∵abc≠0,

∴=+.

∴,,成等差数列.

17.(本小题满分12分)已知函数f(x)=ab^x的图象过点A(4,)和B(5,1).

(1)求函数f(x)的解析式.

(2)记a_n=log₂f(n),n是正整数，S_n是数列{a_n}的前n项和，解关于n的不等式a_nS_n≤0.

(3)对于(2)中的a_n与S_n，整数96是否为数列{a_nS_n}中的项？若是，则求出相应的项数；若不是，则说明理由.

解：(1)由=a·b⁴,1=a·b⁵,得b=4,a=,故f(x)=.

(2)由题意知a_n=log₂(·4ⁿ)=2n－10，

S_n=(a₁+a_n)=n(n－9),

a_nS_n=2n(n－5)(n－9).

由a_nS_n≤0,得(n－5)(n－9)≤0,即5≤n≤9.

故n=5,6,7,8,9.

(3)a₁S₁=64,a₂S₂=84,a₃S₃=72,a₄S₄=40.

当5≤n≤9时，a_nS_n≤0.

当n≥10时，a_nS_n≥a₁₀S₁₀=100.

因此，96不是数列{a_nS_n}中的项.

18.(本小题满分12分)已知f(x+1)=x²－4,等差数列{a_n}中，a₁=f(x－1),a₂=－,a₃=f(x).

(1)求x的值;

(2)求a₂+a₅+a₈+…+a₂₆的值.

解：(1)∵f(x+1)=(x+1－1)²－4=［(x+1)－1］²－4，

∴f(x)=(x－1)²－4.

∴a₁=(x－2)²－4,a₃=(x－1)²－4.

又a₁+a₃=2a₂,解得x=0或x=3.

(2)∵a₁、a₂、a₃分别为0、－、－3或－3、－、0，

∴a_n=－(n－1)或a_n=(n－3).

①当a_n=－(n－1)时，a₂+a₅+…+a₂₆=(a₂+a₂₆)=;

②当a_n= (n－3)时，a₂+a₅+…+a₂₆=(a₂+a₂₆)=.

19.(本小题满分12分)用分期付款方式购买家用电器一件，价格为1150元，购买当天先付150元，以后每月这一天都交付50元，并加付欠款的利息，月利率为1%，若交付150元后的第一个月开始算分期付款的第一个月，问分期付款的第十个月该交付多少钱？全部货款付清后，买这件家电实际花了多少钱？

解：购买时付了150元，欠款1000元，每月付50元，分20次付完.

设每月付款顺次组成数列{a_n}，则

a₁=50+1000×0.01=60(元).

a₂=50+(1000－50)×0.01=(60－0.5)(元).

a₃=50+(1000－50×2)×0.01=(60－0.5×2)(元).

依此类推得

a₁₀=60－0.5×9=55.5(元),

a_n=60－0.5(n－1)(1≤n≤20).

∴付款数{a_n}组成等差数列，公差d=－0.5,全部货款付清后付款总数为

S₂₀+150=(a₁+a₂₀)+150

=(2a₁+19d)×10+150

=(2×60－19×0.5)×10+150

=1255(元).

答：第十个月该交付55.5元，全部货款付清后，买这件家电实际花了1255元.