第三章　数列(一)

●知识网络

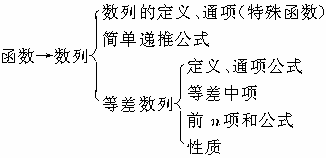
●范题精讲

一、等差数列的概念、通项公式

【例1】 等差数列{a_n}的前n项和记为S_n.已知a₁₀=30,a₂₀=50.

(1)求通项a_n;

(2)若S_n=242,求n.

分析：在等差数列中，有a₁、a_n、n、d、S_n五个基本量，若已知其中的任何三个，总可以求出另外两个的值.

解：(1)由a_n=a₁+(n－1)d,a₁₀=30,a₂₀=50,

得方程组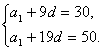

解得a₁=12,d=2.

所以a_n=2n+10.

(2)由S_n=na₁+d,S_n=242,得方程12n+×2=242.

解得n=11或n=－22(舍去).

评注：本题是一个最基础的数列题，内容上只涉及等差数列的通项和前n项和.它主要考查等差数列的通项公式、求和公式以及构造方程的数学方法，考查运算能力.知识点较为单一，但高考中仍不乏这类考查目的明确、适应所有考生的中低档题.

二、等差数列性质的应用

【例2】 已知等差数列{a_n}为等差数列，p≠q,a_p=q,a_q=p,求a_p+q.

分析：可先转化为a₁和d去探索，也可利用等差数列性质求解，还可利用一次函数图象来解.

① ②

解法一：　　　　　　　　　　　　　　　　　　　

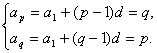
相减得(p－q)d=q－p,∵p≠q,∴d=－1.代入①,

得a₁=p+q－1.故a_p+q=a₁+(p+q－1)d=0.

解法二：a_p=a_q+(p－q)d,∴q=p+(p－q)d,以下同解法一.

解法三：不妨设p<q,由于a_n为关于n的一次函数图象上均匀排列的一群孤立点.故(p,a_p)、(q,a_q)、(p+q,a_p+q)三点在同一直线上，如图.

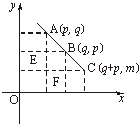
由△ABE∽△BCF得(设a_p+q=m)

∴1=.设m=0,得a_p+q=0.

三、等差数列前n项和公式的应用

【例3】 设等差数列｛a_n｝的前n项和为S_n,已知a₃=12,S₁₂＞0,S₁₃＜0.

(1)求公差d的取值范围;

(2)指出S₁,S₂,…,S₁₂中哪一个值最大，并说明理由.

(1)解：依题意有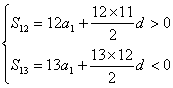

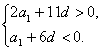
由a₃=12,得a₁=12－2d.

又－＜d＜－3.

(2)解法一：由d＜0,可知a₁＞a₂＞a₃＞…＞a₁₂＞a₁₃.

因此，若在1≤n≤12中，存在自然数n，使得a_n＞0,a_n+1＜0,则S_n就是S₁,S₂,…,S₁₂中的最大值.

由于S₁₂=6(a₆+a₇)＞0,S₁₃=13a₇＜0,即a₆+a₇＞0,a₇＜0,由此得a₆＞－a₇＞0.

故在S₁，S₂，…，S₁₂中S₆的值最大.

解法二：S_n=na₁+d

=n(12－2d)+n(n－1)d=n²－(－12)n

=［n－(5－)］²－［(5－)］².

∵d＜0,∴［n－(5－)］²最小时，S_n最大.

当－＜d＜－3时，6＜(5－)＜6.5.

∴n=6时，［n－(5－)］²最小.

∴S₆最大.

解法三：由d＜0,可知a₁＞a₂＞a₃＞…＞a₁₂＞a₁₃.

因此，若在1≤n≤12中，存在自然数n，使得a_n＞0,a_n+1＜0,则S_n就是S₁,S₂,…,S₁₂中的最大值.

由已知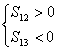

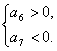
故在S₁,S₂,…,S₁₂中S₆的值最大.

评注：第(2)题用了三种方法来解，解法一与解法三类似，只是确定a₆＞0,a₇＜0的方法不同，解法一技巧性强,解法二是把问题转化成了有限制条件的一元二次函数最值问题.

四、数列的应用

【例4】 某鱼塘养鱼，由于改进了饲养技术，预计第一年产量的增长率为200%，以后每年的增长率是前一年增长率的一半，设此鱼塘里原来的鱼储存量为a.

(1)写出改进饲养技术后的第一年、第二年、第三年、第四年的产量，并写出第n年与第(n－1)年(n∈N且n≥2)的产量之间的关系式(不要求证明).

(2)由于环境污染及池塘老化等因素，致使每年将损失年产量的10%，这样以后每年的产量是否始终逐年提高?若是，请予以证明；若不是，请说明从第几年起产量将不如上一年.(lg2=0.3010,lg3=0.4771)

解：(1)不妨设改进技术后第n年的产量为a_n，则

a₁=a(1+200%)=3a,a₂=a₁(1+×200%)=6a,

a₃=a₂(1+×200%)=9a,a₄=a₃(1+×200%)=a.

依此，得a_n=a_n－1(1+×200%)=a_n－1［1+()^n－2］(n∈N^*,n≥2).

(2)设遭损失后第n年的产量为b_n,则

b₁=a₁(1－10%),b₂=b₁(1+×200%)(1－10%),…,

b_n=b_n－1［1+()^n－2］(1－10%).

令b_n＜b_n－1,则0.9［1+()^n－2］＜12^n－2＞9,

∴n－2＞,即n＞5.17.由n∈N^*知n≥6.

故从第6年起，产量将不如上一年.

评注：这是一道数列型应用题，审题时应抓住从第二年开始，"以后每年的增长率是前一年增长率的一半"这个关键，把它抽象为数列的通项，容易求出递推关系式a_n=a_n－1［1+　()^n－2］(n∈N^*且n≥2),即建成了递推模型.第(2)问归结为一个指数不等式问题，利用取对数法很容易求得这个数学问题的解.

●试题详解

高中同步测控优化训练(十一)

第三章　数列(一)(A卷)

说明：本试卷分为第Ⅰ、Ⅱ卷两部分，共100分，考试时间90分钟.

第Ⅰ卷(选择题　共30分)

一、选择题(本大题共10小题，每小题3分，共30分)

1.在100至500之间的正整数能被11整除的个数为

A.34　　　　　　　　　　　　　　　　　 B.35　　　　　　　　　　　　　　 C.36　　　　　　　　　　　　　　　　　 D.37

解析：观察出100至500之间能被11整除的数为110，121，132，…，它们构成一个等差数列，公差为11，a_n=110+(n－1)·11=11n+99,由a_n≤500,解得n≤36.4,n∈N^*,∴n≤36.

答案：C

2.在数列{a_n}中，a₁=1,a_n+1=a_n²－1(n≥1),则a₁+a₂+a₃+a₄+a₅等于

A.－1　　　　　　　　　　　　　 B.1　　　　　　　　　　　　　　　C.0　　　　　　　　　　　　　　　D.2

解析：由已知：a_n+1=a_n²－1=(a_n+1)(a_n－1),

∴a₂=0,a₃=－1,a₄=0,a₅=－1.

答案：A

3.若数列{a_n}的前n项和S_n=n²－2n+3，则此数列的前3项依次为

A.－1,1,3　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.2,1,3

C.6,1,3　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.2,3,6

解析：当n=1时，a₁=S₁=1²－2×1+3=2;

当n=2时，由S₂=a₁+a₂=2²－2×2+3,得a₂=1;

当n=3时，由S₃=a₁+a₂+a₃=3²－2×3+3,得a₃=3.

答案：B

4.设函数f(x)满足f(n+1)=(n∈N^*)且f(1)=2,则f(20)为

A.95　　　　　　　　　　　　　　　　　 B.97　　　　　　　　　　　　　　 C.105　　　　　　　　　　　　　 D.192

解析：f(n+1)－f(n)=

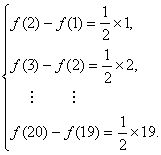
各式相加得f(20)－f(1)=(1+2+…+19) f(20)=95+f(1)=97.

答案：B

5.已知等差数列｛a_n｝中公差d≠0.若n≥2,n∈N^*,则

A.a₁a_n+1＜a₂a_nB.a₁+a_n+1＞a₂+a_n

C.a₁+a_n+1＜a₂+a_nD.a₁a_n+1＞a₂a_n

解析：a₁a_n+1－a₂a_n=a₁(a₁+nd)－(a₁+d)［a₁+(n－1)d］=－(n－1)d²＜0,∴a₁a_n+1＜a₂a_n.

答案：A

6.等差数列｛a_n｝中，a₄+a₇+a₁₀=57,a₄+a₅+…+a₁₄=275,a_k=61,则k等于

A.18　　　　　　　　　　　　　　　　　 B.19　　　　　　　　　　　　　　 C.20　　　　　　　　　　　　　　　　　 D.21

解析：∵3a₇=a₄+a₇+a₁₀=57,∴a₇=19.由a₄+a₅+…+a₁₄=275,可得a₉=25.∴公差d=3.　　　 ∵a_k=a₉+(k－9)·d,∴61=25+(k－9)×3,解得k=21.

答案：D

7.已知等差数列{a_n}的公差为正数，且a₃·a₇=－12,a₄+a₆=－4,则S₂₀为

A.180　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.－180

C.90　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.－90

解析：由等差数列性质，a₄+a₆=a₃+a₇=－4与a₃·a₇=－12联立，即a₃、a₇是方程x²+4x－12=0的两根.又公差d>0,∴a₇>a₃a₇=2,a₃=－6,从而得a₁=－10,d=2,S₂₀=180.

答案：A

8.设S_n是等差数列前n项的和，若,则等于

A.1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.－1

C.2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

解法一：∵,∴=.

∴.

解法二：∵,

∴

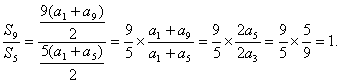
答案：A

9.已知｛a_n｝是递增数列，且对任意n∈N^*都有a_n=n²+λn恒成立，则实数λ的取值范围是

A.(－,+∞)　　　　　　　　　　　　　　　　　　　　　　　　　B.(0,+∞)

C.(－2,+∞)　　　　　　　　　　　　　　　　　　　　　　　　　　 D.(－3,+∞)

解析：由｛a_n｝为递增数列得a_n+1－a_n=2n+1+λ＞0恒成立,即λ＞－2n－1在n≥1时恒成立，只需λ＞(－2n－1)_max=－3,故选D.

答案：D

10.在等差数列{a_n}中，若S₉=18,S_n=240,a_n－4=30,则n的值为

A.14　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.15

C.16　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.17

解析：S₉==18a₁+a₉=42(a₁+4d)=4.

∴a₁+4d=2.又a_n=a_n－4+4d,∴S_n==16n=240.

∴n=15.

答案：B

第Ⅱ卷(非选择题　共70分)

二、填空题(本大题共4小题，每小题4分，共16分)

11.设数列{a_n}的前n项和为S_n,S_n=(n∈N^*),且a₄=54,则a₁的值是________.

解析：∵a₄=S₄－S₃,

∴=54.∴a₁=2.

答案：2

12.若数列｛a_n｝的前n项和S_n=lg［(1+n)］,则a₁₀+a₁₁+a₁₂+…+a₉₉=_________.

解析：a₁₀+a₁₁+…+a₉₉=S₉₉－S₉=lg(·100)－lg(·10)=1－0=1.

答案：1

13.在－9和3之间插入n个数，使这n+2个数组成和为－21的等差数列，则n=_______.

解析：－21=,∴n=5.

答案：5

14.等差数列{a_n}中，a₁+a₂+a₃=－24,a₁₈+a₁₉+a₂₀=78,则此数列前20项的和等于________.

解析：由a₁+a₂+a₃=－24,可得3a₂=－24;

由a₁₈+a₁₉+a₂₀=78,可得3a₁₉=78,即a₂=－8,a₁₉=26.

∴S₂₀==10(a₂₊a₁₉)=10(－8+26)=180.

答案：180

三、解答题(本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤)

15.(本小题满分8分)已知数列｛a_n｝满足下列条件，写出它的前5项，并归纳出数列的一个通项公式.

(1)a₁=0,a_n+1=a_n+(2n－1);

(2)a₁=1,a_n+1=.

解：(1)∵a₁=0,a_n+1=a_n+(2n－1),

∴a₂=a₁+(2×1－1)=0+1=1,a₃=a₂+(2×2－1)=4,a₄=a₃+(2×3－1)=9,a₅=a₄+(2×4－1)=16.

∴它的前5项依次是0，1，4，9，16.又可写成(1－1)²,(2－1)²,(3－1)²,(4－1)²,(5－1)².

故该数列的一个通项公式是a_n=(n－1)².

(2)∵a₁=1,a_n+1=,

∴a₂=,

a₄=

∴它的前5项依次是1,.

又可写成

故它的一个通项公式为a_n=.

16.(本小题满分10分)已知等差数列｛a_n｝中，a₁+a₄+a₇=15,a₂a₄a₆=45,求其通项a_n.

解：∵a₁+a₇=2a₄,且a₁+a₄+a₇=15,∴a₄=5.

又∵a₂a₄a₆=45,∴a₂a₆=9.

设其公差为d,又a₄=5,∴a₂=a₄－2d,a₆=a₄+2d.代入a₂a₆=9可得

(5－2d)(5+2d)=925－4d²=9d=±2.

当d=2时，a_n=a₄+(n－4)d=5+(n－4)×2=2n－3(n∈N^*);

当d=－2时，a_n=a₄+(n－4)d=5+(n－4)×(－2)=13－2n(n∈N^*).

17.(本小题满分12分)数列的通项公式为a_n=n²－5n+4，问:

(1)数列中有多少项是负数？

(2)n为何值时，a_n有最小值？并求出最小值.

解：(1)由a_n为负数，得n²－5n+4<0,解得1<n<4.

∵n∈N^*,故n=2或3，即数列有2项为负数，分别是第2项和第3项.

(2)∵a_n=n²－5n+4=(n－)²－,

∴对称轴为n==2.5.

又∵n∈N^*,故当n=2或n=3时，a_n有最小值，最小值为2²－5×2+4=－2.

18.(本小题满分12分)有30根水泥电线杆，要运往1000米远的地方开始安装，在1000米处放一根，以后每隔50米放一根，一直向前放.一辆汽车一次最多运三根，如果用一辆车完成这项任务，从开始运第一车算起，运完货后回到起点，这辆汽车的行程是多少千米？

解：设在运完第3(n－1)至3n(其中1≤n≤10且n∈N^*)根且返回起点时，这辆汽车的行程为a_n米，则根据题意得a₁=(1000+50+50)×2=2×1100,a₂=(1100+50+50+50)×2=2(1100+150),a₃=(1100+150+50+50+50)×2=2(1100+300),….

∴{a_n}是以2×1100为首项，150为公差的等差数列.从而行程为s₁₀=(1100×10+×10×9×150)×2=35500.

答：这辆汽车的行程是35500千米.

19.(本小题满分12分)设无穷等差数列{a_n}的前n项和为S_n.

(1)若首项a₁=,公差d=1,求满足S_k2=(S_k)²的正整数k;

(2)求所有的无穷等差数列{a_n}，使得对一切正整数k都有S_k2=(S_k)²成立.

解：(1)当a₁=,d=1时，

S_n=na₁+

由S_k2=(S_k)²,得k⁴+k²=(k²+k)²,

即k³(k－1)=0.又∵k≠0,∴k=4.

(2)设等差数列{a_n}的公差为d,则在S_k2=(S_k)²中，分别取k=1,2,得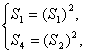

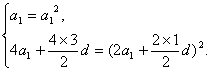
① ②

即

由①得a₁=0或a₁=1.

当a₁=0时，代入②得d=0或d=6.

若a₁=0,d=0,则a_n=0,S_n=0,从而S_k2=(S_k)²成立；

若a₁=0,d=6,则a_n=6(n－1),S_n=3n²－3n.此时S_k2=3k⁴－3k²,(Sk)²=(3k²－3k)²,显然S_k2≠(S_k)².

当a₁=1时，代入②式得d=0或d=2.

若a₁=1,d=0时，a_n=1,S_n=n,从而S_k2=(S_k)²成立；

若a₁=1,d=2时，a_n=2n－1,S_n=1+3+…+(2n－1)=n²,从而S_k2=(S_k)²成立.

综上，共有3个满足条件的无穷等差数列，它们是a_n=0,a_n=1,a_n=2n－1.