三角函数的图象和性质·典型例题
![]()
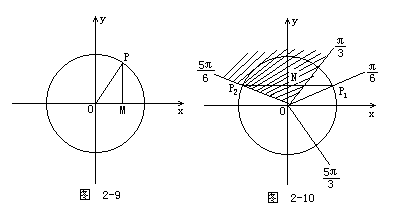
解:在单位圆中,作出锐角α在正弦线MP,如图2-9所示
![]()
在△MPO中,MP+OM>OP=1即MP+OM>1
∴sinα+cosα>1
![]()
![]()
于P1,P2两点,过P1,P2分别作P1M1⊥x轴,P2M2⊥x轴,垂足分
![]()
![]()
![]()
![]()
k∈Z}
![]()
【说明】 学会利用单位圆求解三角函数的一些问题,借助单位圆求解不等式的一般方法是:①用边界值定出角的终边位置;②根据不等式定出角的范围;③在[0,2π]中找出角的代表;④求交集,找单位圆中重叠的部分;⑤写出角的范围的表达式,注意加周期.
【例3】 求下列函数的定义域:
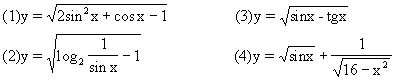
解:(1)为使函数有意义,需满足2sin2x+cosx-1≥0
![]()

![]()

由单位圆,如图2-12所示
![]()
k∈Z}
【说明】 求函数的定义域通常是解不等式组,利用“数形结合”,借助于数轴画线求交集的方法进行.在求解三角函数,特别是综合性较强的三角函数的定义域,我们同样可以利用“数形结合”,在单位圆中画三角函数线,求表示各三角不等式解集的扇形区域的交集来完成.

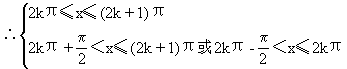
![]()
![]()
(4)为使函数有意义,需满足:

取k=0和-1时,得交集为-4<x≤-π或0≤x≤π
∴函数的定义域为(-4,-π]∪[0,π]
【说明】 求三角函数的定义域要注意三角函数本身的特征和性质,如在转化为不等式或不等式组后要注意三角函数的符号及单调性,在进行三角函数的变形时,要注意三角函数的每一步变形都保持恒等,即不能改变原函数的自变量的取值范围.
【例4】 求下列函数的值域:
![]()
![]()
![]()
![]()
![]()
∴此函数的值域为{y0≤y<1}
![]()
∵1+sinx+cosx≠0 ∴t≠-1
![]()
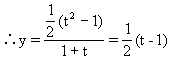
![]()
![]()
![]()
【说明】 求三角函数的值域,除正确运用必要的变换外,还要注意函数的概念的指导作用,注意利用正、余弦函数的有界性.
【例5】 判断下列函数的奇偶性:
![]()
![]()
【分析】 先确定函数的定义域,然后根据奇函数成偶函数的定义判断函数的奇偶性.
![]()
∵f(1-x)=-sin(-2x)=sin2x=-f(x)
![]()
(2)函数的定义域为R,且
f(-x)=sin[cos(-x))=sin(cosx)=f(x)
∴函数f(x)=sin(cosx)是偶函数.
(3)因1+sinx≠0,∴sinx≠-1,函数的定义域为{xx∈R且x≠2k
![]()
既不是奇函数,也不是偶函数.
【例6】 求下列函数的最小正周期:
![]()
【分析】 欲求三角函数的周期,一般是把三角函数f(x)化成易求周期的函数y=Asin(ωx+j)+b或y=Acos(ωx+j)+b的等形式.函数y=Asin(ω
![]()
![]()
“多个化一个,高次化一次”,将所给函数化成单角单函数.
![]()
![]()
(2)y=cos4x+sin4x=(cos2x+sin2x)2-2sin2xcos2x
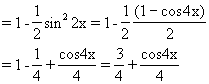
![]()
![]()
![]()
=cosx+sinx=f(x)
![]()
正周期.
![]()
(x+T)+cos(x+T)=sinx+cosx都成立.特别当x=0时,有sinT+cosT=sinT
![]()
![]()
【例8】 求下列各函数的最大值、最小值,并且求使函数取得最大值、最小值的x的集合.

![]()
![]()
∴使y取得最大值的x的集合为{xx=(2kπ+1)π,k∈Z}
![]()
∴使y取得最小值的x的集合为{xx=2kπ,k∈Z}
![]()
![]()
当cosx=1,即x=2kπ(k∈Z)时,y取得最大值3.
![]()
![]()
![]()
【说明】 求三角函数的最值的类型与方法:
1.形如y=asinx+b或y=acosx+b,可根据sinx,cosx的有界性来求最值;
2.形如y=asin2x+bsinx+c或y=acos2x+bcosx+c看成是关于sinx或cosx的二次函数,变为y=a(sinx+m)2+k或y=a(cosx+m)2+k,但要注意它与二次函数求最值的区别,此时sinx≤1,cosx≤1
![]()
![]()
【例9】 求下列函数的单调区间:
![]()
【分析】 复杂三角函数的单调区间是运用基本函数的单调性及单调区间得出的.

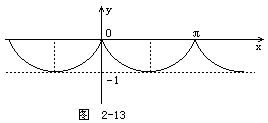
![]()
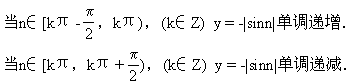
![]()
![]()
![]()
![]()
(2)函数y=sin2x-2sinx+2,是由y=u2-2u+2及u=sinx及复合而成,∴u≤1

![]()
![]()
【例10】 当a≥0,求函数f(x)=(sinx+a)(cosx+a)的最大值、最小值,及相应的x的取值.
【分析】 本题对f(x)解析式的变换关键在于认识解析式中两项间的内在联系,从而断定f(x)解析式中的平方关系,另外本题含字母系数,要分清常数和变量,还要有对字母a作分类讨论的准备.
解:f(x)=(sinx+a)(cosx+a)=sinxcosx+a(sinx+cosx)+a2
![]()
![]()
![]()
由于a是常数,故这里只要求y=(sinx+cosx+a)2的最大值、最小值.合
![]()
![]()
物线的图象如图2-14所示两种可能.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
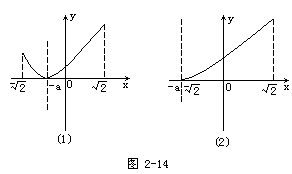
![]()
![]()
![]()
![]()
![]()
【说明】 象本例这种解析式中含字母系数的函数研究其性质,常常要运用分类讨论的思想,其中为什么要分类,怎么分类和讨论是两个基本问题.
【例11】 函数f(x)=Asin(ωx+j)的图象如图2-15,试依图指出
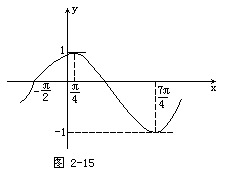
(1)f(x)的最小正周期;
(2)使f(x)=0的x的取值集合;
(3)使f(x)<0的x的取值集合;
(4)f(x)的单调递增区间和递减区间;
(5)求使f(x)取最小值的x的集合;
(6)图象的对称轴方程;
(7)图象的对称中心.
【分析】 这是一道依图象读出相应函数性质的典型例题,本身就是数形结合思想的体现,它根据f(x)=Asin(ωx+j)的图象与函数y=sinx的图象的关系得出.
![]()
注:得出函数f(x)的最小正周期之后,研究f(x)的其他性质,总是先在包含锐角在内的一个周期中研究,再延伸到整个定义域中.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
注:实际上f(x)图象的对称轴方程为x=x0,而其中x0使f(x0)=1或f(x0)=-1
![]()
注:f(x)的图象的对称中心为(x0,0),其中x0使f(x0)=0
【说明】 这种依图读性的问题是提高数形结合能力的重要训练题,其中有两点要注意反思:①周期性在研究中的化简作用,②三角函数的“多对一”性.
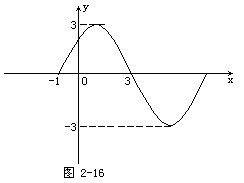
【例12】 求如图2-16所示的函数解析式.(ω>0,θ∈[0,2π])
【分析】 由图象确定函数的解析式,就要观察图象的特性,形状位置和所给的条件.通过判断、分析和计算确定A,ω、θ得到函数的解析式.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
【例13】 设y=Asin(ωx+j)(A>0,ω>0,j<π)最高点D的
![]()
标为(6,0),(1)求A、ω、j的值;(2)求出该函数的频率,初相和单调区间.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
y单调递增故递增区间为[16k-6,16k+2],k∈Z
![]()
y单调递减故递减区间为[16k+2,16k+10],k∈Z
![]()
A.sinθ<cosθ<ctgθ
B.cosθ<sinθ<ctgθ
C.sinθ<ctgθ<cosθ
D.cosθ<ctgθ<sinθ
解一(直接法):
![]()
![]()
![]()
故选A.
解二(图解法):
作出三角函数线,如图2-17
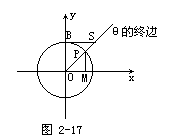
MP=sinθ,OM=cosθ,BS=ctgθ
通过观察和度量得MP<OM<BS
从而有sinθ<cosθ<ctgθ
∴应选A
![]()
∴cosθ>sinθ
从而可剔除B、D.
再由sinθ<ctgθ,故可剔除C
故选A
解四(特殊值法):
![]()
B、C、D,应选A.
【说明】 此例题用多种方法求解选项,指出3种选择题的技巧.
![]()

![]()
![]()
∴应选D
![]()
x轴交点中在原点右边最接近原点的交点,而在原点左边与x轴交点中最
![]()
![]()
的图象.
∴选D
【说明】 y=Asin(ωx+j)(A>0,ω>0)x∈R的图象可由y=sinx的图象经下列各种顺序变换得到的.
(1)先平移,后伸缩:
①把y=sinx的图象向左(j>0)或向右(j<0)沿x轴方向平移j个单位;(相位变换)
![]()
(周期变换)
③把所有各点纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍,横坐标不变(振幅变换)
(2)先伸缩,后平移
①把y=sinx图象上各点的横坐标缩短(ω>1)或伸长(0<ω<1)到原
![]()
![]()
(相位变换)
③把所有各点纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍横坐标不变(振幅变换)
![]()
再把横坐标缩小到原来的一半,纵坐标扩大到原来的4倍,则所得的图象的解析式是 [ ]

![]()

∴选A.
【例17】 方程sin2x=sinx在区间(0,2π)内解的个数是
[ ]
A.1 B.2 C.3 D.4
【分析】 本题有两类解法
(1)求出方程在(0,2π)内的所有解,再数其解的个数.而决定选项,对于选择题,此法一般不用.
(2)在同一坐标系中作出函数y=sin2x和y=sinx的图象,如图2-18所示.
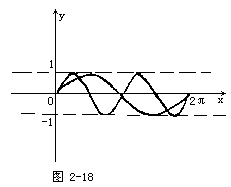
它们在(0,2π)内交点个数,即为所求方程解的个数,从而应选C.
![]()
![]()
它体现了数、形的结合.
【例18】 设函数f(x)是定义在R上的周期为3的奇函数,且f(1)=2,则f(5)=____
解:∵f(x)是奇函数,且f(1)=2,∴f(-1)=-2
又∵f(x)是周期为3的函数. ∴f(3+x)=f(x)
∴f(-1+3)=f(-1)=-2 即f(2)=-2
f(2+3)=f(2)=-2 即f(5)=-2
【例19】 有一块扇形铁板,半径为R,圆心角为60°,从这个扇形中切割下一个内接矩形,即矩形的各个顶点都在扇形的半径或弧上,求这个内接矩形的最大面积.
【分析】 本题入手要解决好两个问题.
(1)内接矩形的放置有两种情况,如图2-19所示,应该分别予以处理.
(2)求最大值问题这里应构造函数,怎么选择便于以此表达矩形面积的自变量.

解:如图2-19(1)设∠FOA=θ,则FG=Rsinθ
![]()
![]()
又设矩形EFGH的面积为S,那么
![]()
![]()
又∵0°<θ<60°,故当cos(2θ-60°)=1,即θ=30′时,
![]()
如图2-19 (2),设∠FOA=θ,则EF=2Rsin(30°-θ),在△OFG中,∠OGF=150°
![]()
设矩形的面积为S.
那么S=EFFG=4R2sinθsin(30°-θ)
=2R2[cos(2θ-30°)-cos30°]
![]()
又∵0<θ<30°,故当cos(2θ-30°)=1
![]()
![]()
![]()