交集、并集·典型例题
能力素质
例1 已知M={yy=x2+1,x∈R},N={yy=-x2+1,x∈R}则M∩N是
[ ]
A.{0,1} B.{(0,1)}
C.{1} D.以上均不对
分析 先考虑相关函数的值域.
解 ∵M={yy≥1},N={yy≤1},
∴在数轴上易得M∩N={1}.选C.
![]()
取值范围是
[ ]
A.m<4 B.m>4
C.0<m<4 D.0≤m<4
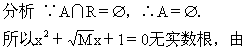
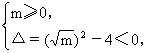
可得0≤m<4.
答 选D.
例3 设集合A={x-5≤x<1},B={xx≤2},则A∪B=
[ ]
A.{x-5≤x<1} B.{x-5≤x≤2}
C.{xx<1} D.{xx≤2}
分析 画数轴表示
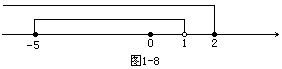
![]()
B).
答 选D.
说明:集合运算借助数轴是常用技巧.
例4 集合A={(x,y)x+y=0},B={(x,y)x-y=2},则A∩B=________.
分析 A∩B即为两条直线x+y=0与x-y=2的交点集合.
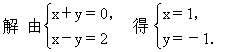
所以A∩B={(1,-1)}.
说明:做题之前要搞清楚集合的元素是什么.
![]()
∪B);
![]()
为
[ ]
A.1 B.2
C.3 D.4
分析 根据交集、并集的定义,①是错误的推理.
答 选C.
点击思维
例6 已知全集U=R,A={x-4≤x<2},B={x-1<x
![]()
=________.
![]()
号的值.
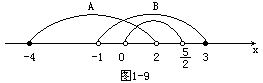
解 观察数轴得,A∩B={x-1<x<2},A∩B∩(![]() UP)={x0<x<2}.
UP)={x0<x<2}.
例7 设A={x∈Rf(x)=0},
B={x∈Rg(x)=0},
![]()
[ ]
A.C=A∪(![]() UR) B.C=A∩(
UR) B.C=A∩(![]() UB)
UB)
C.C=A∪B D.C=(![]() UA)∩B
UA)∩B
分析 依据分式的意义及交集、补集的概念逐步化归
![]()
={x∈Rf(x)=0且g(x)≠0}
={x∈Rf(x)=0}∩{x∈Rg(x)≠0}=A∩(![]() UB).
UB).
答 选B.
说明:本题把分式的意义与集合相结合.
例8 集合A含有10个元素,集合B含有8个元素,集合A∩B含有3个元素,则集合A∪B有________个元素.
分析 一种方法,由集合A∩B含有3个元素知,A,B仅有3个元素相同,根据集合元素的互异性,集合A∪B的元素个数为10+8-3=15.
另一种方法,画图1-10观察可得.
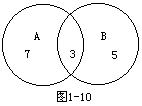
答 填15.
例9 已知全集U={xx取不大于30的质数},A,B是U的两个子集,且A∩(![]() UB)={5,13,23},(
UB)={5,13,23},(![]() UA)∩B={11,19,29},(
UA)∩B={11,19,29},(![]() UA)∩(
UA)∩(![]() UB)={3,7}求A,B.
UB)={3,7}求A,B.
分析 由于涉及的集合个数,信息较多,所以可以通过画图1-11直观地求解.

解 ∵U={2,3,5,7,11,13,17,19,23,29}
用图形表示出A∩(![]() UB),(
UB),(![]() UA)∩B及(
UA)∩B及(![]() UA)∩(
UA)∩(![]() UB)得
UB)得
![]() U(A∪B)={3,7},A∩B={2,17},所以
U(A∪B)={3,7},A∩B={2,17},所以
A={2,5,13,17,23},
B={2,11,17,19,29}.
说明:对于比较复杂的集合运算,可借助图形.
学科渗透
例10 设集合A={x2,2x-1,-4},B={x-5,1-x,9},若A∩B={9},求A∪B.
分析 欲求A∪B,需根据A∩B={9}列出关于x的方程,求出x,从而确定A、B,但若将A、B中元素为9的情况一起考虑,头绪太多了,因此,宜先考虑集合A,再将所得值代入检验.
解 由9∈A可得x2=9或2x-1=9,解得x=±3或5.
当x=3时,A={9,5,-4},B={-2,-2,9},B中元素违反互异性,故x=3应舍去;
当x=-3时,A={9,-7,-4},B={-8,4,9},A∩B={9}满足题意,此时A∪B={-7,-4,-8,4,9}
当x=5时,A={25,9,-4},B={0,-4,9},此时A∩B={-4,9},这与A∩B={9}矛盾.
故x=5应舍去.
从而可得x=-3,且A∪B={-8,-4,4,-7,9}.
说明:本题解法中体现了分类讨论思想,这在高中数学中是非常重要的.
例11 设A={xx2+4x=0},B={xx2+2(a+1)x+a2-1=0},若A∩B=B,求a的值.
![]()
需要对A的子集进行分类讨论.
![]()
设0∈B,则a2-1=0,a=±1,当a=-1时,B={0}符合题意;当a=1时,B={0,-4}也符合题意.
设-4∈B,则a=1或a=7,当a=7时,B={-4,-12}不符合题意.
![]()
<-1.
综上所述,a的取值范围是a≤-1或a=1.
![]()
高考巡礼
例12(1998年全国高考题)设集合M={x-1≤x<2},N={xx
![]()
[ ]
A.(-∞,2] B.[-1,+∞)
C.(-1,+∞) D.[-1,2]
分析 分别将集合M、N用数轴表示,可知:k≥-1时,M∩
![]()
答 选B.
例13(2000年全国高考题)如图1-12:U为全集,M、P、S是U的3个子集,则下图中的阴影部分为________.

分析 利用交集、并集、补集的意义分析.
解 阴影部分为:(M∩P)∩(![]() US).
US).
说明:你能否指出M∩(P∪S)是图形上的哪一区域?