等差数列·例题解析

 

【例1】　在100以内有多少个能被7个整除的自然数？

解　∵100以内能被7整除的自然数构成一个等差数列，其中a₁=7，d＝7，a_n＝98．

代入a_n＝a₁＋(n－1)d中，有

98＝7＋(n－1)·7

解得n＝14

答　100以内有14个能被7整除的自然数．

【例2】　在－1与7之间顺次插入三个数a，b，b使这五个数成等差数列，求此数列．

解　设这五个数组成的等差数列为{a_n}

由已知：a₁＝－1，a₅＝7

∴7＝－1＋(5－1)d　解出d＝2

所求数列为：－1，1，3，5，7．

插入一个数，使之组成一个新的等差数列，求新数列的通项．

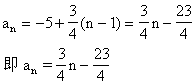
【例4】　在[1000，2000]内能被3整除且被4除余1的整数共有多少个？

解　设a_n=3n，b_m＝4m－3，n，m∈N

得n＝4k－1(k∈N)，得{a_n}，{b_m}中相同的项构成的数列{c_n}的通项c_n＝12n－3(n∈N)．

则在[1000，2000]内{c_n}的项为84·12－3，85·12－3，…，166·12－3

∴n＝166－84＋1=83　∴共有83个数．

【例5】　三个数成等差数列，其和为15，其平方和为83，求此三个数．

解　设三个数分别为x－d，x，x＋d．

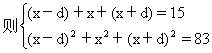
解得x＝5，d＝±2

∴ 所求三个数为3、5、7或7、5、3

说明　注意学习本题对三个成等差数列的数的设法．

【例6】　已知a、b、c成等差数列，求证：b＋c，c＋a，a＋b也成等差数列．

证　∵a、b、c成等差数列

∴2b=a＋c

∴(b＋c)＋(a＋b)＝a＋2b＋c

＝a＋(a＋c)＋c

＝2(a＋c)

∴b＋c、c＋a、a＋b成等差数列．

说明　如果a、b、c成等差数列，常化成2b＝a＋c的形式去运用；反之，如果求证a、b、c成等差数列，常改证2b=a＋c．本例的意图即在让读者体会这一点．

可能是等差数列．

分析　直接证明a、b、c不可能是等差数列，有关等差数列的知识较难运用，这时往往用反证法．

证　假设a、b、c是等差数列，则2b=a＋c

∴2ac＝b(a＋c)=2b²，b²＝ac．

又∵ a、b、c不为0，

∴ a、b、c为等比数列，

又∴ a、b、c为等差数列，

∴ a、b、c为常数列，与a≠b矛盾，

∴ 假设是错误的．

∴ a、b、c不可能成等差数列．

【例8】　解答下列各题：

(1)已知等差数列{a_n}，a_n≠0，公差d≠0，求证：

①对任意k∈N，关于x的方程

a_kx²＋2a_k+1x＋a_k+2＝0有一公共根；

分析与解答

(1)a_kx²＋2a_k+1x＋a_k+2＝0

∵{a_n}为等差数列，∴2a_k+1＝a_k＋a_k+2

∴a_kx²＋(a_k＋a_k+2)x＋a_k+2＝0

∴(a_kx＋a_k+2)(x＋1)=0，a_k≠0

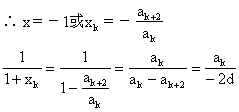
∵{a_n}为等差数列，d为不等于零的常数

(2)由条件得　2b=a＋c

∴4RsinB＝2RsinA＋2RsinC，2sinB＝sinA＋sinC

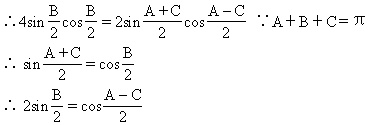
分析至此，变形目标需明确，即要证

由于目标是半角的余切形式，一般把切向弦转化，故有

【例9】　若正数a₁，a₂，a₃，…a_n+1成等差数列，求证：

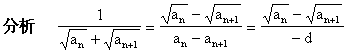
证明　设该数列的公差为d，则

a₁－a₂=a₂－a₃＝…＝a_n－a_n+1=－d

∴a₁－a_n+1=－nd

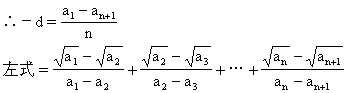
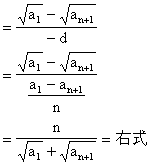
∴ 原等式成立．

【例10】　 设x≠y，且两数列x，a₁，a₂，a₃，y和b₁，x，