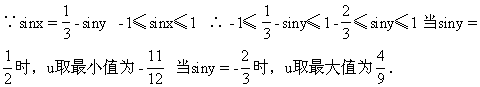三角函数的图象和性质·基础练习题
一、选择题
![]()
[ ]
![]()
B.A=B
![]()
答:C
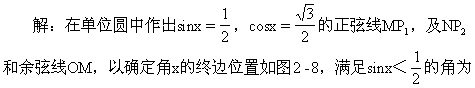



[ ]
A.y=x2(x∈R)
B.y=sinx(x∈R)
C.y=cos2x(x∈R)
D.y=esin2x(x∈R)
答:B
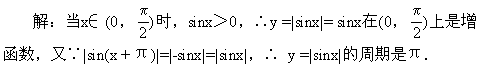
93.如果α,β都是第二象限的角,且α>β,那么 [ ]
A.sinα>sinβ
B.sinβ>sinα
C.sinα≥sinβ
D.不能确定大小
答:D

94.下列函数中不是周期函数的是 [ ]
A.y=-8π
B.y=cosx
![]()
D.y=sinx
答:D
解:从y=sinx的图象(图2-9)可以看出不存在一个非零常数T,使sinx+T=sinx对任何x∈R都成立,∴ y=sinx不是周期函数.

95.函数y=cos(sinx)的值域是 [ ]
A.〔cos(-1),cos1〕
B.〔-1,1〕
C.〔cos1,1〕
D.〔1,cos1〕
答:C
解:∵-1≤sinx≤1 ∴cos1≤cos(sinx)≤1值域为〔cos1,1〕.
96.若θ为第二象限角,则必有 [ ]


答:C
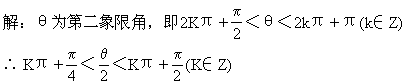
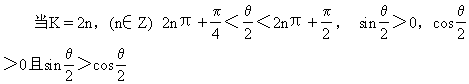

![]()
[ ]
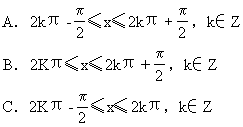
D.x∈R
答:D
解:要使函数有意义cos(sinx)≥0
![]()
![]()
[ ]
A.A为锐角
B.A为钝角
C.A为锐角或钝角
D.A可能是钝角
答:A


![]()
[ ]

C.-1
![]()
答:D

100.已知集合M={xsinx=1},集合N={xsinx=1},则M与N间的关系是 [ ]
![]()
C.M=N
![]()

答:A
解:画出y=sinx及y=sinx的图象如图2-10



101.下列结论中正确的是 [ ]
A.当x为第二象限角时,y=sinx和y=tgx都是减函数
B.余切函数y=ctgx在整个定义域内是减函数
![]()
D.函数y=tgx在它的一个周期内是增函数
答:C
解:象限不能作为单调区间,所以A.错误;余切函数的定义域不是单调区间,y=tgx在一个周期内,不一定是增函数,所以排除B.、D.;

102.设α、β都是第二象限角,若sinα>sinβ,则 [ ]
A.tgα>tgβ
B.ctgα<ctgβ
C.cosα>cosβ
D.secα>secβ
答:C
解:∵α、β为第二象限角,又sinα>sinβ且sinα>sinβ>0.∴sin2α>sin2β,1-cos2α>1-cos2β ∴cos2α<cos2βcosα<cosβ又∵cosα、cosβ都为负 ∴-cosα<-cosβ ∴cosα>cosβ。
103.函数y=tgx是 [ ]
A.周期为π的奇函数
B.周期为π的偶函数

答:B
解:∵ tg(-x)=-tgx=tgx∴y=tgx是偶函数,又∵tg(x+π)=tgx ∴y=tgx的周期为π.
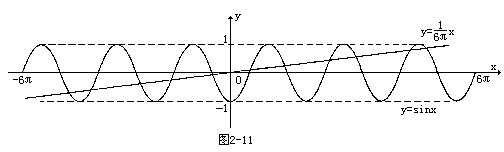
104.方程6πsinx=x的解的个数是 [ ]
A.9个
B.10个
C.11个
D.12个
答:C
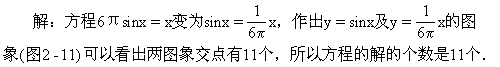
![]()
[ ]
A.第三象限或第四象限

答:B

106.函数f(x)=sin2x-sinxcosx+cos2x的最大值是
[ ]
![]()
B.1
![]()
D.0
答:A
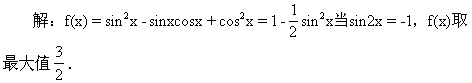

[ ]
A.13
B.12
C.11
D.10
答:A

![]()
[ ]



答:B

![]()
109.直线y=a(a为常数)与正切曲线y=tgωx(ω为常数且ω>0)相交,相邻两点间的距离是 [ ]
A.π
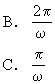
D.与a值有关
答:C
解:直线y=a与正切曲线y=tgωx相交的两相邻交点间距离为y=
![]()
二、填空题
![]()
![]()
解:要使函数有意义,必须



![]()


答:-1
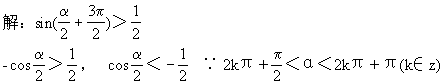


113.已知sinα<cosα.则α的取值范围是____
![]()
解:由单位圆中的正弦线、余弦线可以看出,若sinα<cosα,则


答:0
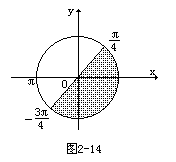

115.函数y=cos2x-3cosx+2的最小值是______
答:0
![]()
上变化,∴关于cosx的二次函数在〔-1,1〕上是减函数,当cosx=1,y取最小值0.
![]()
系是______
答:α>β
![]()
![]()
117.若f(cosx)=cos17x 则f(sinx)=______
答:sin17x
![]()
![]()
![]()
![]()
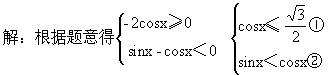
由单位圆的阴影部分可确定x的终边的范围是
![]()
三、解答题
119.求下列函数的定义域:
![]()
![]()
![]()
![]()
![]()
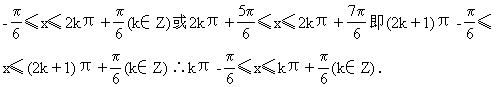

120.求下列函数的值域
![]()
![]()
![]()
![]()
![]()
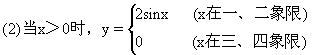

![]()
![]()

![]()
![]()

122.作出函数y=tg2xctgx的图象,写出它的单调区间.

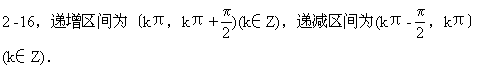
![]()

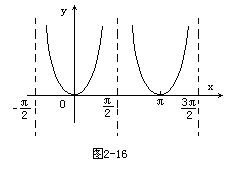

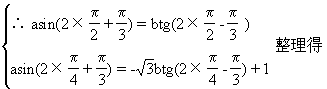
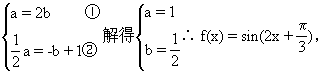
![]()
![]()
![]()
![]()