期中检测题

　

(一)选择题

1．下列四句话表示集合的是

[　]

A．一切很大的数　　　 　B．好心的人

C．所有小于10的质数　　　　　　D．我国大城市

2．不等式2x＋5≤7的解集是

[　]

A．{x－6＜x＜1}　　　 　B．{xx＜－6或x＞1}

C．{x－6≤x≤1}　　　 　D．{xx≤－6或x≥1}

3．下列命题①5＞2且7＞3，②3＞4或3＜4，③7≥8，④方程x²－3x＋4＝0的判别式小于0或等于0，其中真命题的个数是

[　]

A．一个　　　 　　B．二个

C．三个　　　 　　D．四个

4．设非空集合A、B、C，若“a∈A”的充要条件是“a∈B且a∈C”，那么“a∈B”是“a∈A”的

[　]

A．充要条件　　　 　B．必要不充分条件

C．充分不必要条件　　　　D．既不充分也不必要条件

[　]

A．(0，＋∞)

B．(－∞，0)

C．(－∞，－1)∪(－1，0)

D．(－∞，－1)∪(－1，0)∪(0，＋∞)

[　]

A．[0，1]　　 　B．[1，2]

C．[－1，1] 　　D．[0，2]

7．设f(x)(x∈R)为偶函数且f(x)在[0，＋∞)上是增函数，则f(－2)、f(－π)、f(3)的大小顺序是

[　]

A．f(－π)＞f(3)＞f(－2)　 　　　B．f(－π)＞f(－2)＞f(3)

C．f(－π)＜f(3)＜f(－2)　 　　　D．f(－π)＜f(－2)＜f(3)

b、c的值是

[　]

A．a=3，b＝2，c＝1

B．a＝－3，b=1，c＝2

C．a=1，b=2，c＝－3

D．a=1，b＝－3，c=2

9．已知f(x)＝x¹⁵＋ax¹¹＋bx⁷＋8且f(－2)＝10，则f(2)的值是

[　]

A．6　　　　B．－6

C．8　　　　D．－8

10．如果0＜a＜1下列不等式中正确的是

[　]

A．(1－a)³＞(1＋a)²　　　　B．(1－a)^1+a＞1

(二)填空题

11．函数y=2(x²－2x)＋3在区间[0，3]上的最大值是________，最小值是________．

实数a的取值范围是________．

________．

15．已知函数f(x)存在反函数，a是它定义域的任意的一个值，则f^-1[f(a)]=________．

三、解答题

2．设a≠b，解关于x的不等式：

a²x＋b²(1－x)≥[ax＋b(1－x)]²

域上的单调性．

4．定义在(－1，1)上的奇函数f(x)是减函数且f(1－a)＋f(1－a²)＜0，求实数a的取值范围．

5．已知f(x)＝x²－x＋k，且log₂f(a)＝2，f(log₂x)＝k(a≠1)．

(1)求f(log₂a)的最小值及对应的x的值．

(2)x为何值时，f(log₂x)＞f(1)且log₂f(x)＜f(1)．

参考答案

 

(一)选择题

1．(C)．</PGN0214B.TXT/PGN>

3．(C)．

解：①、②、④命题为真，∴选C

4．(B)．

∴选B．

5．(C)．

且x≠－1，∴选(C)．

6．(B)．

7．(A)．

解：∵f(x)为偶函数，∴f(－2)=f(2)，f(－π)=f(π)，又∵f(x)在[0，＋∞)上是增函数，0＜2＜3＜π，∴f(2)＜f(3)＜f(π)∴选A．

8．(C)．

比较对应项的系数得a=1　c=－3　b=2　∴选C．

9．(A)．</PGN0215A.TXT/PGN>

∴f(2)=2¹⁵＋a2¹¹＋b2⁷＋8=6．

10．(C)．

解：∵0＜a＜1，0＜1－a＜1，1＜1＋a＜2，∴(1－a)³＜1，(1＋a)²＞1

则(1－a)³＜(1＋a)²．(A)错．

∴(1－a)^(1+a)＜1，则(B)错．

(二)填空题

11．9，1．

解：∵y=2(x－1)²＋1　x∈(0，3]．

当x=3时，y_max=9，当x=1时，y_min=1．

12．(－1，＋∞)

解：A={x－1＜x＜2}，A∩B≠

∴a＞－1．

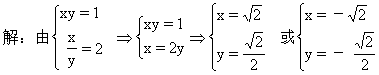
14．(－∞，1)和(1，＋∞)

15．a

解：设f(a)=b，则f^-1(b)=a，∴f^-1[f(a)]=f^-1(b)=a．

(三)解答题

=(x－1)²＋1

f^-1(x)的图像如右图．

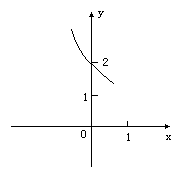
2．解：原不等式化为：

a²x＋b²(1－x)≥a²x²＋2abx(1－x)＋b²(1－x)²

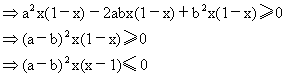
∵a≠b．∴(a－b)²＞0，∴x(x－1)≤0

∴0≤x≤1为不等式的解．

3．分析：令u=x²＋1，则u在x∈(－∞，0]上为，在x∈[0，

证：定义域为R，设x₁，x₂∈R且x₁＜x₂

∵x₁，x₂∈R，x₁＜x₂，x₁²＋1＞0，x₂²＋1＞0，x₂－x₁＞0</PGN0216A.TXT/PGN>

(1)当x₁，x₂∈(－∞，0]时，x₁＋x₂＜0

∴f(x₁)－f(x₂)＜0，f(x₁)＜f(x₂)

∴f(x)在(－∞，0]上为增函数．

(2)当x₁，x₂∈(0，＋∞)时，x₁＋x₂＞0，

∴f(x₁)＞f(x₂)

∴f(x)在(0，＋∞)上为减函数．

4．解：∵f(1－a)＋f(1－a²)＜0

∴ f(1－a)＜－f(1－a²)

又∵f(x)是奇函数．∴f(1－a)＜f(1－a²)

又∵f(x)在(－1，1)上是减函数．

5．解：(1)由f(log₂a)=log₂²a－log₂a＋k=k．

得log₂a(log₂a－1)=0，∵a≠1，

∴log₂a≠0，只有log₂a=1，∴a=2

又log_af(a)=log_a(a²－a＋k)=log_a(2＋k)=2，∴k=2，于是

由①、②得0＜x＜1为所求．