1　函数的单调性·基础练习

 

(一)选择题

[　　]

A．增函数

B．既不是增函数又不是减函数

C．减函数

D．既是增函数又是减函数

[　　]

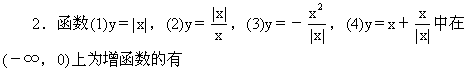
A．(1)和(2)　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　B．(2)和(3)

C．(3)和(4)　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　D．(1)和(4)

3．若y＝(2k－1)x＋b是R上的减函数，则有

[　　]

4．如果函数f(x)＝x²＋2(a－1)x＋2在区间(－∞，4]上是减函数，那么实数a的取值范围是

[　　]

A．a≥－3　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　B．a≤－3

C．a≤5　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　D．a≥3

5．函数y＝3x－2x²＋1的单调递增区间是

[　　]

6．若y＝f(x)在区间(a，b)上是增函数，则下列结论正确的是

[　　]

B．y＝－f(x)在区间(a，b)上是减函数

C．y＝f(x)²在区间(a，b)上是增函数

D．y＝f(x)在区间(a，b)上是增函数

7．设函数f(x)是(－∞，＋∞)上的减函数，则

[　　]

A．f(a)＞f(2a)　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．f(a²)＜f(a)

C．f(a²＋a)＜f(a)　　　　　　　　　　　　 　　　　　　　　　　D．f(a²＋1)＜f(a)

(二)填空题

3．函数y＝4x²－mx＋5，当x∈(－2，＋∞)时，是增函数，当x∈(－∞，－2)时是减函数，则f(1)＝________．

6．函数f(x＋1)＝x²－2x＋1的定义域是[－2，0]，则f(x)的单调递减区间是________．

7．已知函数f(x)是区间(0，＋∞)上的减函数，那么f(a²－a＋1)

ax²＋bx在(0，＋∞)上是________函数(填增还是减)．

(三)解答题

3．已知函数f(x)＝2x²＋bx可化为f(x)＝2(x＋m)²－4的形式．其中b＞0．求f(x)为增函数的区间．

4．已知函数f(x)，x∈R，满足①f(1＋x)＝f(1－x)，②在[1，＋∞]上为增函数，③x₁＜0，x₂＞0且x₁＋x₂＜－2，试比较f(－x₁)与f(－x₂)的大小关系．

参考答案

(一)选择题

1．(B)．

④两函数在(－∞，0)上是增函数．

3．(B)．解：若y=(2k－1)x＋b是R上的减函数，则2k－1＜0

6．(B)．解：可举一例y=x在x∈(－∞，＋∞)上是增函数，从而否定了(A)、(C)、(D)．∴选(B)．

∞，＋∞)上为减函数，∴f(a²＋1)＜f(a)，选(D)．

(二)填空题

1．(－∞，1)和(1，＋∞)

区间是(－∞，－1)和(－1，＋∞)．

5，故f(1)=25．

是(－∞，－3]．

6．[－1，1]．解：令t=x＋1，∵－2≤x≤0，∴－1≤t≤1，∴f(t)=(t－1)²－2(t－1)＋1=t²－4t＋4，即f(x)=x²－4x＋4=(x－2)²在区间[－1，1]上是减函数．

8．减解；由已知得a＜0，b＜0，二次函数y=ax²＋bx的抛物

(三)解答题

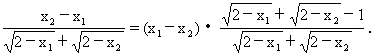
＞1，x₁－x₂＜0．

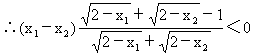
在区间(－∞，－b)和(－b，＋∞)上都是减函数．

3．解：∵f(x)=2(x＋m)²－4=2x²＋4mx＋2m²－4．

由题意得2x²＋bx=2x²＋4mx＋2m²－4，对一切x恒成立，比较

4．解：∵x₁＜0，x₂＞0，x₁＋x₂＜－2，∴－x₁＞2＋x₂＞1，即－x₁，2＋x₂∈[1，＋∞)，又f(x)在[1，＋∞)上为增函数，∴f(－x₁)＞f(2＋x₂)，又由f(1＋x)=f(1－x)，得f(2＋x₂)=f[1＋(1＋x₂)]=f[1－(1＋x₂)]=f(－x₂)．

∴f(－x₁)＞f(－x₂)．