北大附中2001—2002学年高一下学期数学期末考试
2002年7月3日
邓军
班张:____________ 姓名:_________ 成绩:__________
一、选择题(下列各题只有一个选项是正确的,请把正确选项的序号填写在答题卡上对应的位置,每个小题3分,共14小题,计42分)
1.设A,B,C是△ABC的三个内角,且tgA,tgB是方程![]() 的两个实数根,那么△ABC是()
的两个实数根,那么△ABC是()
(A)钝角三角形(B)锐角三角形
(C)等腰直角三角形(D)等边三角形
2.已知α为锐角,![]() ,则cosα的值等于()
,则cosα的值等于()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
3.函数![]() 的最大值是()
的最大值是()
(A)4(B)![]()
(C)6(D)![]()
4.将函数![]() 的图象作如下那种变换,才能得到函数
的图象作如下那种变换,才能得到函数![]() 的图象?()
的图象?()
(A)向右平移![]() (B)向左平移
(B)向左平移![]()
(C)向右平移![]() (D)向左平移
(D)向左平移![]()
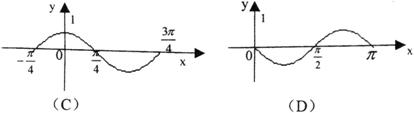
5.函数![]() 在同一个周期内的图象是()
在同一个周期内的图象是()

6.函数![]() 的最小正周期是()
的最小正周期是()
(A)2π(B)π
(C)![]() (D)
(D)![]()
7.函数![]() 的值域是()
的值域是()
(A)(-4,0](B)[-4,0)
(C)[-4,0](D)[0,4]
8.圆台的侧面面积是它内切球表面积的![]() 倍,则圆台母线和底面所成的角的大小是()
倍,则圆台母线和底面所成的角的大小是()
(A)30°(B)45°
(C)60°(D)75°
9.圆锥侧面展开图是一个半径为12的半圆,则这个圆锥的内切球体积是()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
10.如果轴截面为正方形的圆柱的侧面积为S,那么圆柱的体积为()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
11.长方体的一个顶点上的三条棱分别为3,4,5,且它的八个顶点都在同一个球面上,这个球的表面积是()
(A)![]() (B)
(B)![]()
(C)50π(D)200π
12.圆锥的侧面积为8π,侧面展开图的圆心角是![]() ,则圆锥的体积为()
,则圆锥的体积为()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
13.正四棱锥P-ABCD中,高PO的长是底面长的![]() ,且它的体积等于
,且它的体积等于![]() ,则棱AB与侧面PCD之间的距离是()
,则棱AB与侧面PCD之间的距离是()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
14.在△ABC中,3sinA+4cosB=6,3cosA+4sinB=1,则角C的大小为()
(A)![]() (B)
(B)![]()
(C)![]() 或
或![]() (D)
(D)![]() 或
或![]()
二、填空题(请把你认为的正确答案填写在答题卡的对应项内,每小题3分,共12分)
15.函数![]() 的最大值是______最小值是________。
的最大值是______最小值是________。
16.设f(x)是以5为周期的奇函数,f(-3)=1,又tgα=3,则![]()
17.在棱长为2的正方体![]() 中,对角线
中,对角线![]() 在六个面上的射影长度总和为____
在六个面上的射影长度总和为____
18.一个棱台两底面积分别为18和128,一个平行于两底的截面将棱台的高分为1:2的两部分,则此截面的面积为_______
三、解答题(需要写出详细的解题过程,共46分)
19.求cos55°·cos65°+cos65°·cos175°+cos55°·cos175°的值。
20.在△ABC中,a,b,c分别表示三个内角A,B,C的对边,如果满足条件![]() ,且A≠B,求证:△ABC是直角三角形。
,且A≠B,求证:△ABC是直角三角形。
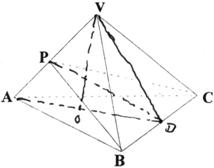
21.如图,正三棱锥V-ABC的底面边长为a, 侧棱与底面所成的角等于θ,过底面一边作棱锥的截面,当截面与底面所成二面角为何值时,截面面积最小?并求出最小值。
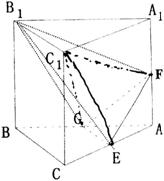
22.如图,在直三棱柱![]() 中,
中,![]() ,∠ACB=90°,E,F,G分别为AC,
,∠ACB=90°,E,F,G分别为AC,![]() ,AB的中点,(1)求证:
,AB的中点,(1)求证:![]() 平面EFG(2)求三棱锥
平面EFG(2)求三棱锥![]() 的体积。
的体积。
北大附中2001-2002学年高一下学期数学期末考试参考答案
一、选择题(每题3分共计42分)
1A 2A 3C 4C 5D 6C 7A 8C 9B
10D 11C 12A 13A 14A
二、填空题:(每题3分共计12分)
15. 0,-8
16.-1
17.![]()
18.![]()
三、解答题(共46分)
19.原式![]() 和差化积 积化和差4分
和差化积 积化和差4分
![]()
![]() 整理2分
整理2分
![]() 积化和差2分
积化和差2分
![]()
![]() 结果2分
结果2分
20.证:原式化为![]()
![]() 整理2分
整理2分
![]()
![]() 正整理2分
正整理2分
∵0<B<π,0·A<π ∴sinA≠0, sinB≠0
∴sinAcosA=sinBsinB. sin2A=sin2B 整理2分
sin2A-sin2B=0 和差化积2分
∴2cos(A+B)·sin(A-B)=0
∵A-B≠0 ∴sin(A-B) ≠0
∴cos(A+B)=0 整理2分
∴sinC=0
∴c=90°
∴△ABC是直角三角形 结果2分
21.解:作VO⊥平面ABC,O为垂足,因为V-ABC是正三棱锥,所以O为△ABC的中心,连结AO并延长交BC于D则AD⊥BC,∠DAO=θ连VD,Pθ
∴BC⊥VA ∴BC⊥平面VAD PDC平面VAD 证明4分
∴PD⊥BC ∴∠PDA为截面与底面所成角,设为x,在△PAD中,∠PAD=θ,∠PDA=x,∴∠APD=180°-(θ+π) 写出4分
根据连结定理![]()
 4分
4分
当且仅当sin(θ+x)=1,θ+x=90°,x=90°-θ的等号成立,∴PD最小
∴![]() 最小面积
最小面积![]()
![]()
解法2 ∵截面△PBC中,BC=a为定值,∴![]() ,若是S最小,只须PD最小即可,
,若是S最小,只须PD最小即可,
∵VA,BC为异面直线,∴当PD为异面直线VA,BC的公垂线时,PD最短。
∴当PD⊥BC,PD⊥VA时,PD最短,在Rt△APD中,∵![]()
∴![]() ,∴
,∴![]()
22.解:(1)E,F为△AB,AC中点,∴GE∥BC。
∵![]() ,∴
,∴![]() ,
,
∵![]() 平面GEF,
平面GEF,![]() 平面GEF,
平面GEF,
∴![]() 平面EFG 4分
平面EFG 4分
(2)∵![]() 平面EFG,∴
平面EFG,∴![]() 与
与![]() 到平面EFG的距离相等。 2分
到平面EFG的距离相等。 2分
∴![]() 2分
2分
∵![]() ,
,![]() ,
,![]() ∴
∴![]() 平面
平面![]()
∵![]() ∴GE⊥平面
∴GE⊥平面![]() 2分
2分
∵![]()
![]()
![]() 2分
2分
∴![]() 1分
1分