2000学年度第一学期高一年级

　　数学学科期中测试题

　　一、填空题（每小题3分，共30分）

　　1、用列举法表示集合，则A=________。

　　2、设全集I={1，2，3，4，5，6，7}，集合A={1，3，5，7}B={2，3，5，7}，则。

　　3、设全集I=R，集合，B={x x-2<2}，则A∪B =________。

　　4、设集合A={x0<x<2},B={xx<a},若，则实数a 的取值范围是_________。

　　5、设全集，集合A={5，a+1}，则a=_______。

　　6、若x,y∈R则的一个充要条件是________。

　　7、设A是B的充分非必要条件，B是C的充要条件，C是D的充分非必要条件，则D是A的_______条件。

　　8、不等式的解集是_________。

　　9、不等式1≤x-2≤7的解集是_________。

　　10、已知扇形的周长为8cm，则这个扇形的最大面积是_______.

　　二、选择题（每小题4分，共20分）

　　11、已知集合M={（x,y）x+y=4}, N=(x,y)x-y=2},则集合M∩N是 （　　）

　　A、x=3,y=1 B、(3,1) C、{(3,1)} D、{3,1}

　　12、已知集合P={xx=n,n∈Z},,，则有（　　）

　　A、　　B、　C、　D、

　　13、设集合A={xx<2,x∈R},B={xx<4,x∈R}，则“x∈A∩B”是“x∈A或x∈B”的（　 ）

　　A、充分非必要条件B、必要非充分条件C、充要条件D、既非充分又非必要条件

　　14、一元二次方程有一个正根和一个负根的充要条件是（　　 ）

　　A、　B、　C、　D、

　　15、已知a>b>0，那么下列各式正确的是（　　）

　　A、 B、 C、 D、

　　三、解答题（每小题7分，共21分）

　　16、（7分）设a，b，，试比较与的大小。

　　17、（7分）已知原命题：“△ABC中，BD、CE分别是边AC、AB上的中线，若BD≠CE则AB≠AC。”

　　（1）写出原命题的逆命题，否命题，逆否命题。

　　（2）判断原命题的真假，并证明你的结论。

　　18、（7分）

　　解不等式

　　四、解答题（每小题7分，共21分）

　　19、（7分）实数k在什么范围内取值时，不等式的解集是实数集R？

　　解集会不会是空集？说明理由。

　　20、（7分）设集合，，若，求a的取值范围。

　　21、（7分）

　　（一般中学）当m为何值时，关于x的方程m(x-3)=3(x+1)的解在区间[1，2]内。

　　（重点中学）设a,b,c∈（0，1）

　　（1）证明：a+b<ab+1

　　（2）证明：a+b+c<abc+2

　　（3）试猜想出更一般的结论（不要求证明）。

　　五、应用题

　　22、（8分）

　　·（一般中学）某居民小区的蓄水池容量足够大，现有水40吨，自来水厂每小时可向蓄水池中注水8吨，同时蓄水池又向居民小区供水，t小时内供水总量为吨。现在开始向池中注水并同时向居民小区供水，若蓄水池中存水量少于10吨，就会出现供水紧张现象，问供水多长时间开始出现供水紧张，这一天内供水紧张的时间有几小时？（提示：可设）

　　·（重点中学）某地区上年度电价为0.7元/kw·h(度)，年用电量为akw·h，本年度供电量充足有余，电力部门计划将电价降到0.55元/kw·h至0.65元/kw·h之间，而用户期望电价为0.4元/kw·h。经测算，下调电价后，新增的用电量与实际电价和用户期望电价的差成反比，比例系数为0.1a。该地区电力的成本为0.2元/kw·h，问电价最低定为多少时，仍可保证电力部门的收益比上年至少增加20%？

　　

　　

　　

　　高一数学参考答案及评分标准

　　一、填空题

　　1、{2，-1，-2}；2、{1，2，4，6}；3、{x-1<x<4}；4、a≥2；5、2；6、x≠0或y≠0；7、必要非充分；8、（1，2 ）；9、[-5，1]∪[3，9]；10、4

　　二、选择题

　　11、C； 12、D； 13、A； 14、D； 15、B

　　三、解答题（每小题7分，共21分）

　　16、作差（3分）

　　∵a,b,∴b+a>0,b(bc+a)>0(1分)

　　∴当a<b时，；当a=b时，；

　　当a>b时，（3分）

　　17、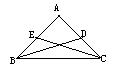

　　（1）逆命题：△ABC中，BC、CE分别是边AC、AB上的中线，若AB≠AC，则BD≠CE。

　　否命题：△ABC中，BD、CE分别是边AC、AB上的中线，若BD=CE，则AB=AC。

　　逆否命题：△ABC中，BD、CE分别是边AC、AB上的中线，若AB=AC，则BD=CE。（3分）

　　（2）原命题是真命题，往证逆否命题是真命题。

　　　　 

　　，即逆否命题正确。

　　由于原命题与逆否命题是等价命题，故原命题是真命题。（4分）

　　18、或（2）（2分）

　　（1）式（2分）

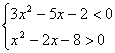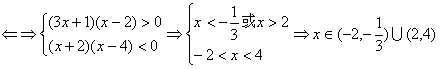　　（2）式（2分）

　　∴原不等式的解集是（1分）

　　四、解答题（每小题7分，共21分）

　　19、设

　　（1）当k=0时，f(x)=2，∴f(x)>0在R上恒成立

　　（2）当k≠0时，的解集是R的充要条件为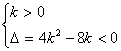（1分）

　　解得0<k<2 (3分)

　　综上，当k∈[0，2）时，不等式的解集为R。（1分）

　　的解集为φ的充要条件为

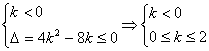　　∴k∈φ,不等式组无解。

　　故不等式的解集不可能是空集。（2分）

　　20、

　　∵∴B可能是{2，3}，{2}，{3}，φ。（1分）

　　（1）当B={2，3}=A时，方程的两根是2和3，

　　∴a=-（2+3）=-5

　　（2）当B={2}或{3}时，方程有一根（相等二实根），∴，，此时方程的根为与B={2}或{3}矛盾，即，∴，即a无解。（2分）

　　（3）当B=φ时，方程无实根。

　　∴∴

　　综上所述，a的取值范围是或a=-5（2分）

　　21、·（一般中学）原方程化为（m-3）x=3m+3（1分）

　　（1）当m=3时，方程无解（1分）

　　（2）当m≠3时，方程的解为，由x∈[1，2]，得

　　

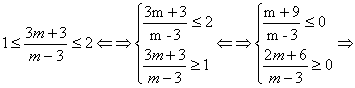
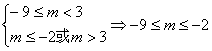　　，即当m∈[-9，-2]

　　时，方程的解在[1，2]内。（5分）

　　·（重点中学）（1）∵a,b∈（0，1）∴a-1<0, 1-b>0

　　∴a+b-(ab+1)=a(1-b)-(1-b)-(1-b)=(a-1)(1-b)<0

　　∴a+b<ab+1（3分）

　　(2)∵a,b,c∈（0，1） ∴ab∈(0，1)由（1）得

　　a+b+c<ab+1+c<abc+1+1=abc+2。（2分）

　　（3）猜想：一般地，若，，，…，

　　则有（2分）

　　五、应用题

　　22、·（一般中学）t小时后蓄水池内的存水量为。

　　令（4分）

　　

　　∴

　　即2.25<t<6.25 （2分）

　　答：供水2.25小时时，开始出现供水紧张，直至6.25小时，一天内有6.25-2.25=4小时供水紧张

　　·（重点中学）设下调后的电价为x元/kw·h，则新增电量为，电力部门的年收益为（1分）

　　依题意得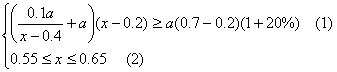（3分）

　　解不等式（1），

　　

　　（x-0.3）(x-0.2)≥0.6(x-0.4)

　　 (3)

　　解得x≤0.5或x≥0.6。(2分)

　　由（2），（3）得0.6≤x≤0.65（1分）

　　答：当最低电价定为0.6/元kw·h时，仍可保证电力部门的年收益比上年至少增加20%。（1分）