弧度制·典型例题分析

　

角度与弧度的换算要熟练掌握，见下表．

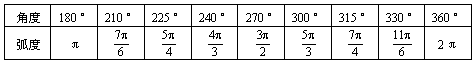
例2　将下列各角化成2kπ+α(k∈Z，0≤α＜2π)的形式，并确定其所在的象限。

∴它是第二象限的角．

注意：用弧度制表示终边相同角2kπ+α(k∈Z)时，是π的偶数倍，而不是π的整数倍．

A．第一象限　　　　　　　　　 B．第二象限

C．第三象限　　　　　　　　　 D．第四象限

∴sinα＞0，tgα＜0

因此点P(sinα，tgα)在第四象限，故选D．

解　∵M集合是表示终边在第一、二、三、四象限的角平分线上的角的集合．

N集合是表示终边在坐标轴(四个位置)上和在第一、二、三、四象限的角平分线上的角的集合．