函数·典型例题分析
例1 与函数y=x表示相同函数的是 [ ]
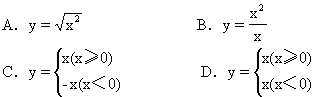
![]()

则、值域不同,排除C.而

评注 判断两个函数是否相同,要看函数的三要素:定义域,值域,对应法则.其中对应法则不能仅仅从解析式上考虑,要分析其对应法则的本质.
例2 求下列函数的定义域


(5)设f(x)的定义域为[0,2],求函数f(x+a)+f(x-a)(a>0)的定义域.

∴定义域是空集,函数是虚设的函数
(2)由函数式可得

∴函数的定义域是{xx=-1},定义域是一个孤立的点(-1,0)的横坐标
(3)∵x2-4≠0
∴x≠±2
∴函数定义域为(-∞,-2)∪(-2,+2)∪(2,+∞)
(4)从函数式可知,x应满足的条件为

∴函数的定义域为
![]()
(5)∵f(x)定义域为[0,2]
所以f(x+a)+f(x-a)中x应满足

又∵a>0,若2-a≥a,则a≤1
即0<a≤1时,f(x+a)+f(x-a)的定义域为{xa≤x≤2-a}
当a>1时,x∈Æ
评注 求f(x)的定义域就是求使函数f(x)有意义的x的取值范围,定义域表示法有:不等式法,集合法,区间表示法等.
例3 求下列函数的值域
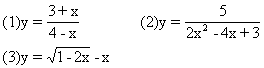
解 (1)由原式可化为
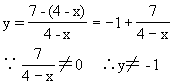
![]()
(2)将函数变形,整理可得:
2yx2-4yx+3y-5=0
当y=0时,-5=0不可能,故y≠0
∵x∈R
∴Δ=(-4y)2-4×2y×(3y-5)≥0
即y(y-5)≤0解得0≤y≤5
而y≠0
∴0<y≤5
故函数值域为(0,5]
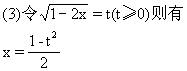
![]()
此二次函数对称轴为t=-1

评注 求函数值域方法很多,此例仅以三个方面给出例子.学习时要分析函数式的结构特征,从而确定较简单的求值域的方法.
例4 (1)已知f(x)=x2,g(x)为一次函数,且y随x值增大而增大.若
f[g(x)]=4x2-20x+25,求g(x)的解析式
![]()
解 (1)∵g(x)为一次函数,且y随x值增大而增大
故可设g(x)=ax+b(a>0)
∵f[g(x)]=4x2-20x+25
∴(ax+b)2=4x2-20x+25
即:a2x2+2abx+b2=4x2-20+25
解得 a=2,b=-5
故g(x)=2x-5
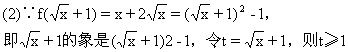
于是有t的象是t2-1,即f(t)=t2-1(t≥1)
故f(x)=x2-1(x≥1)
∴f(x+1)=(x+1)2-1=x2+2x(x≥0)
f(x2)=x4-1(x≤-1或x≥1)
评注 对于(1)是用待定系数法求函数的解析式,要根据题意设出函数的形式,再利用恒等式的性质解之.求函数解析式的常用方法还有拼凑法,代换法(如(2)),解方程组等.
例5 如图1-7,灌溉渠的横断面是等腰梯形,底宽及两边坡总长度为a,边坡的倾角为60°.

(1)求横断面积y与底宽x的函数关系式;
![]()
![]()
![]()
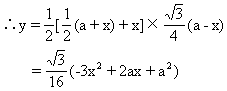
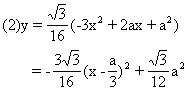

评注 本题是有关函数的实际问题,其方法是把实际问题用数学的形式表示出来,建立变量之间的函数关系.
例6 设x≥0时,f(x)=2,x<0时,f(x)=1又
![]()
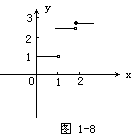
解 当0<x<1时,x-1<0,x-2<0
![]()
当1≤x<2时,x-1≥0,x-2<0
![]()
当x≥2时,
g(x)=2
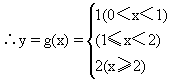
评注 分段函数关键是在x的不同条件下计算方法不同,不要认为是三个不同函数.