含绝对值的不等式解法·典型例题
能力素质
例1 不等式8-3x>0的解集是
[ ]

![]()
答 选C.
例2 绝对值大于2且不大于5的最小整数是
[ ]
A.3 B.2
C.-2 D.-5
分析 列出不等式.
解 根据题意得2<x≤5.
从而-5≤x<-2或2<x≤5,其中最小整数为-5,
答 选D.
例3 不等式4<1-3x≤7的解集为________.
分析 利用所学知识对不等式实施同解变形.
解 原不等式可化为4<3x-1≤7,即4<3x-1≤7或-7
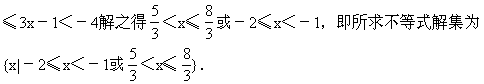
例4 已知集合A={x2<6-2x<5,x∈N},求A.
分析 转化为解绝对值不等式.
解 ∵2<6-2x<5可化为
2<2x-6<5


![]()
因为x∈N,所以A={0,1,5}.
说明:注意元素的限制条件.
例5 实数a,b满足ab<0,那么
[ ]
A.a-b<a+b
B.a+b>a-b
C.a+b<a-b
D.a-b<a+b
分析 根据符号法则及绝对值的意义.
解 ∵a、b异号,
∴ a+b<a-b.
答 选C.
例6 设不等式x-a<b的解集为{x-1<x<2},则a,b的值为
[ ]
A.a=1,b=3
B.a=-1,b=3
C.a=-1,b=-3
![]()
分析 解不等式后比较区间的端点.
解 由题意知,b>0,原不等式的解集为{xa-b<x<a+b},由于解集又为{x-1<x<2}所以比较可得.

答 选D.
说明:本题实际上是利用端点的位置关系构造新不等式组.
例7 解关于x的不等式2x-1<2m-1(m∈R)
分析 分类讨论.
![]()
![]()
![]()
x<m.

{x1-m<x<m}.
说明:分类讨论时要预先确定分类的标准.
点击思维
![]()
分析 一般地说,可以移项后变形求解,但注意到分母是正数,所以能直接去分母.
解 注意到分母x+2>0,所以原不等式转化为2(3-x)≥x+2,整理得
![]()
说明:分式不等式常常可以先判定一下
分子或者分母的符号,使过程简便.
例9 解不等式6-2x+1>1.
分析 以通过变形化简,把该不等式化归为ax+b<c或ax+b>c型的不等式来解.
解 事实上原不等式可化为
6-2x+1>1
①
或 6-2x+1<-1
②
由①得2x+1<5,解之得-3<x<2;
由②得2x+1>7,解之得x>3或x<-4.
从而得到原不等式的解集为{xx<-4或-3<x<2或x>3}.
说明:本题需要多次使用绝对值不等式的解题理论.
例10 已知关于x的不等式x+2+x-3<a的解集是非空集合,则实数a的取值范围是________.
分析 可以根据对x+2+x-3的意义的不同理解,获得多种方法.
解法一 当x≤-2时,不等式化为-x-2-x+3<a即-2x+1<a有解,而-2x+1≥5,
∴a>5.
当-2<x≤3时,不等式化为x+2-x+3<a即a>5.
当x>3是,不等式化为x+2+x-3<a即2x-1<a有解,而2x-1>5,∴a>5.
综上所述:a>5时不等式有解,从而解集非空.
解法二 x+2+x-3表示数轴上的点到表示-2和3的两点的距离之和,显然最小值为3-(-2)=5.故可求a的取值范围为a>5.
解法三 利用m+n>m±n得
x+2+x-3≥(x+2)-(x-3)=5.
所以a>5时不等式有解.
说明:通过多种解法锻炼思维的发散性.
例11 解不等式x+1>2-x.
分析一 对2-x的取值分类讨论解之.
解法一 原不等式等价于:
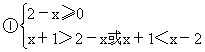



由②得x>2.
![]()
分析二 利用绝对值的定义对x+1进行分类讨论解之.
解法二 因为

原不等式等价于:
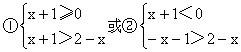
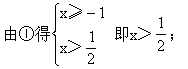
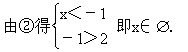
![]()
学科渗透
例12 解不等式x-5-2x+3<1.
分析 设法去掉绝对值是主要解题策略,可以根据绝对值的意义分
![]()
![]()
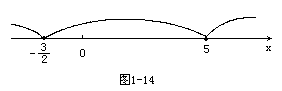
![]()
-(x-5)+(2x+3)<1,得x<-7,所以x<-7;
![]()
-(x-5)-(2x+3)<1,
![]()
当x>5时,原不等式可化为
x-5-(2x+3)<1,
解之得x>-9,所以x>5.
![]()
说明:在含有绝对值的不等式中,“去绝对值”是基本策略.
例13 解不等式2x-1>2x-3.
分析 本题也可采取前一题的方法:采取用零点分区间讨论去掉绝
![]()
之,则更显得流畅,简捷.
解 原不等式同解于
(2x-1)2>(2x-3)2,
即4x2-4x+1>4x2-12x+9,
即8x>8,得x>1.
所以原不等式的解集为{xx>1}.
说明:本题中,如果把2x当作数轴上的动坐标,则2x-1>2x-3表示2x到1的距离大于2x到3的距离,则2x应当在2的右边,从而2x>2即x>1.
