对数函数·例题解析

 

域．

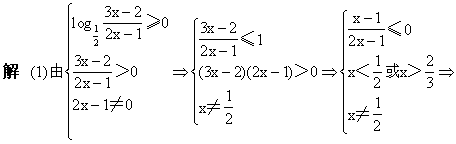
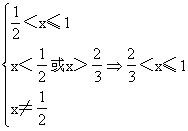
解　(2)∵1－log_a(x＋a)＞0，∴log_a(x＋a)＜1．

当a＞1时，0＜x＋a＜a，∴函数的定义域为(－a，0)．

当0＜a＜1时，x＋a＞a，∴函数的定义域为(0，＋∞)．

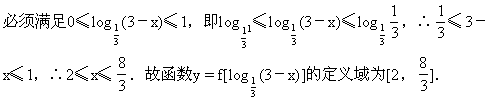
域和值域．

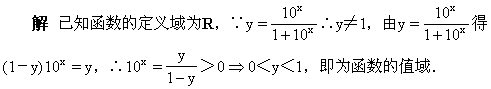
反函数的定义域为(0，1)，值域为y∈R．

【例3】　作出下列函数的图像，并指出其单调区间．

(1)y=lg(－x)，(2)y=log₂x＋1

解　(1)y=lg(－x)的图像与y=lgx的图像关于y轴对称，如图2．8－3所示，单调减区间是(－∞，0)．

解　(2)先作出函数y=log₂x的图像，再把它的图像向左平移1个单位就得y＝log₂x＋1的图像如图2．8－4所示．

单调递减区间是(－∞，－1)．

单调递增区间是(－1，＋∞)．

的图像，保留其在x轴及x轴上方部分不变，把x轴下方的图像以x轴为

所示．

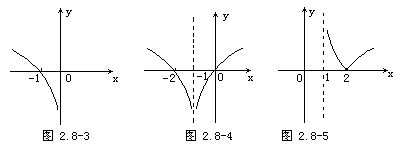
单调减区间是(－1，2]．

单调增区间是[2，＋∞)．

解　(4)∵函数y=log₂(－x)的图像与函数y=log₂x的图像关于y轴对称，故可先作y=log₂(－x)的图像，再把y＝log₂(－x)的图像向右平移1个单位得到y=log₂(1－x)的图像．如图2．8－6所示．

单调递减区间是(－∞，1)．

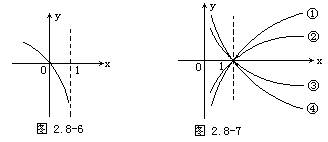
【例4】　图2．8－7分别是四个对数函数，①y=log_ax②y=log_bx③y=log_cx④y=log_dx的图像，那么a、b、c、d的大小关系是

[　]

A．d＞c＞b＞a　　B．a＞b＞c＞d

C．b＞a＞d＞c　　D．b＞c＞a＞d

解　选C，根据同类函数图像的比较，任取一个x＞1的值，易得b＞a＞1＞d＞c．故选C．

【例5】　已知log_a3＞log_b3，试确定a和b的大小关系．

解法一　令y₁=log_ax，y₂=log_bx，∵log_ax＞log_b3，即取x＝3时，y₁＞y₂，所以它们的图像，可能有如下三种情况：

(1)当log_a3＞log_b3＞0时，由图像2．8－8，取x=3，可得b＞a＞1．

(2)当0＞log_a3＞log_b3时，由图像2．8－9，得0＜a＜b＜1．

(3)当log_a3＞0＞log_b3时，由图像2．8－10，得a＞1＞b＞0．

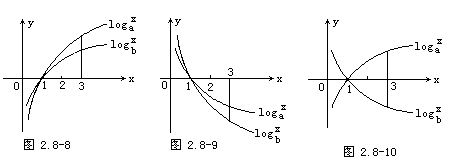
解法二  由换底公式，化成同底的对数．

∵函数y=log₃x为增函数，∴b＞a＞1．

∵函数y=log₃x为增函数，∴0＜a＜b．

即a＞1＞b＞0．

顺序是：________．

说明  本题解决的思路，是把已知的对数值的正负，或大于1，小于1分组，即借助0、1作桥梁这个技巧，使问题得以解决．

【例7】　设0＜x＜1，a＞1，且a≠1，试比较log_a(1－a)与log_a(1＋x)的大小．

解法一　求差比大小．

log_a(1－x)－log_a(1＋x)

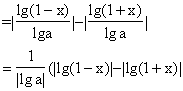
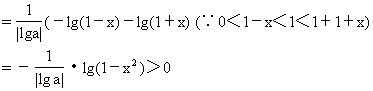
∴log_a(1－x)＞log_a(1＋x)

解法二  求商比较大小

=log_(1+x)(1－x)=－log_1+x(1－x)

∵(1＋x＞1，而0＜1－x＜1)

∴log_a(1－x)＞log_a(1＋x)

奇偶性．

解法一　已知函数的定义域为R，则－x∈R

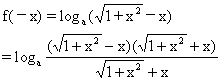
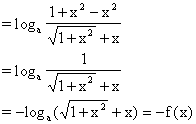
∴f(x)是奇函数．

解法二　已知函数的定义域为R

=log_a1=0

∴f(x)=－f(x)，即f(x)为奇函数．

还是减函数？并证明．

(2)讨论函数y=log_a(a^x－1)的单调性其中a＞0，且a≠1．

(1)证明　方法一  f(x)在(0，1)上是增函数．

设任取两个值x₁，x₂∈(0，1)，且x₁＜x₂．

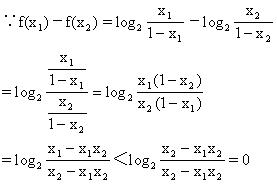
(∵0＜x₁＜x₂＜1，∴x₁－x₁x₂＜x₂－x₁x₂)．

∴f(x₁)＜f(x₂)

故f(x)在(0，1)上是增函数．

(2)解　由对数函数性质，知a^x－1＞0，即a^x＞1，于是，当0＜a＜1时，函数的定义域为(－∞，0)，当a＞1时，定义域为(0，＋∞)．

当0＜a＜1时，u＝a^x－1在(－∞，0)上是减函数，而y=log_au也是减函数，∴y=log_a(a^x－1)在(－∞，0)上是增函数．

当a＞1时，u＝a^x－1在(0，＋∞)上是增函数，而y=log_au也是增函数，∴y＝log_a(a^x－1)在(0，＋∞)上是增函数．

综上所述，函数y=log_a(a^x－1)在其定义域上是增函数．

【例10】　(1)设0＜a＜1，实数x、y满足log_ax＋3log_xa－log_xy=3，

减函数．

＋∞)上是减函数．