本章自测题(二)

　

(一)选择题

1．已知映射f：M→N使集合N中的元素y=x²与集合M中的元素x对应，要使映射f：M→N是一一映射，那么M、N可以是

[　]

A．M＝R，N＝R，　　　　B．M=R，N={yy≥0}

C．M={xx≥0}，N=R　　　 D．M={xx≥0}，N＝{yy≥0}

2．下列各组函数中，表示同一函数的是

[　]

3．下列函数中，在区间(0，2)上为增函数的是

[　]

A．y=3－x　　B．y=x²＋1

C．y=－x²　　D．y=x²－2x＋3

4．y=f(x)是定义在R上的偶函数，则下列坐标所表示的点在y=f(x)的图像上的是

[　]

A．(a，－f(a))　　 　B．(－a，f(a))

C．(－a，－f(－a))　　 D．(－a，－f(a))

5．已知y＝f(x)是奇函数，当x＞0时，f(x)＝x(1＋x)，当x＜0时，f(x)等于

[　]

A．－x(1－x)　　　 　B．x(1－x)

C．－x(1＋x)　　　 　D．x(1＋x)

6．若函数y=mx＋2与y=nx＋3互为反函数，则m、n的值为

[　]

[　]

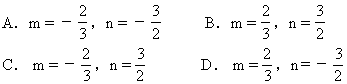
A．y=1＋2^-x(x∈R)　　　　　　B．y=1－2^-x(x∈R)

C．y=1＋2^x(x∈R)　　　D．y=1－2^x(x∈R)

[　]

A．{xx＞1} 　　B．{xx≤2}

C．{x1＜x＜2}　 　　　D．{x1＜x≤2}

9．已知a＞0且a≠1，函数y=a^x与y=log_a(－x)的图像可能是

[　]

[　]

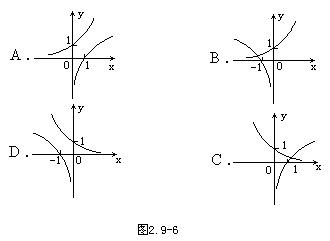
A．f(x)和g(x)都是增函数

B．f(x)和g(x)都是减函数

C．f(x)是减函数，g(x)是增函数

D．f(x)是增函数，g(x)是减函数

11．函数y=log₇(x²＋2x－3)的定义域是

[　]

A． [－3，1]

B．(－3，1)

C．(－∞，－3)∪(1，＋∞)

D．(－∞，－1)∪(3，＋∞)

12．某服装商贩同时卖出两套服装，卖出价为168元／套，以成本计算，一套盈利20％，而另一套亏损20％，则此商贩

[　]

A．不赚也不赔　　　　　B．赚37.2元

C．赚14元　　　D．赔14元

(二)填空题

14．计算lg25＋lg2·lg50＋(lg2)²＝________．

(三)解答题

x＞0时，g(x)=f^-1(x)．

求g(x)的表达式．

18．讨论y=ax³的单调性，并证明你的结论．

(1)求a值．

(2)求f(x)的反函数f^-1(x)．

①求f(x)的定义域．

②判断f(x)的奇偶性，并予以证明．

③当0＜a＜1时，求使f(x)＞0的x的取值范围．

21．某商品的市场日需求量Q₁和日产量Q₂均为价格P的函数，且

①当Q₁＝Q₂时的价格为均衡价格，求此均衡价格P₀．

②当Q₁＝Q₂时，日利润l最大，求l(精确到个位)(已知lg6=0.7781，lg2=0.3010)．

参考答案

 

(一)选择题

1．D．解：在(A)、(B)中，对集合含M中的两个不同元素如x=1与x=－1，在集合N中有相同的象1，在(C)中，对集合N中的元素为负数如y=－1，在集合M中没有原象，∴(A)、(B)、(C)都不满足一一映射定义只有(D)满足一一映射定义，故选(D)．

2．C．解：(A)中f(x)的定义域为R，g(x)的定义域是{xx∈R且x≠－1}，两者定义域不同，∴是不同函数．(B)中f(x)的定义域是x≠0，g(x)的定义域是R，也是定义域不同，∴是不同函数．(C)中(x)与g(x)的定义域相同都为R，对应法则也相同，∴是同一个函数．(D)中两函数的定义域不同，是不同函数．∴选(C)．</PGN0212A.TXT/PGN>

3．B．解：(A)中函数y=3－x在(0，2)上是减函数，(C)中函数y=－x²在(0，2)中是减函数，(D)中函数y=x²－2x＋3在(0，2)上既不是增也不是减．只有(B)中函数y=x²＋1在(0，2)上是增函数．∴选(B)．

4．(B)．解：当x=－a时，f(－a)=f(a)(∵y=f(x)为偶函数)，∴点(－a，f(a))在y=f(x)的图像上．∴选(B)．

5．(B)．解：当x＜0时，f(x)=－f(－x)=－(－x)(1－x)=x(1－x)．∴选(B)．

6．(A)．解：若m=0时，函数y=mx＋2=2是常数函数，而常数函

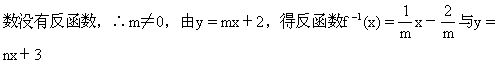
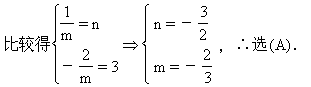
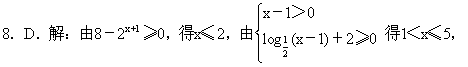
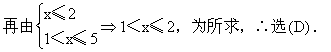
9．B．解：当a＞1时，(A)、(C)、(D)三个都错，只有(B)是对的．

10．(A)．解：用赋值法易确定(A)对．</PGN0212B.TXT/PGN>

12．(D)．解：设第一件成本为a，第二件成本为b，则有a(1＋20％)=168，b(1－20％)=168，解得a=140，b=210，那么两件服装的成本费共为a＋b=350，两件服装卖出共为168×2=336，由a＋b－336=14元．即成本费高出卖出的钱，因此赔了14元．∴选D．

(二)填空题

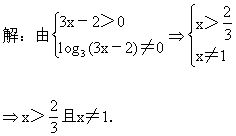
14．2．

=2lg5＋(1－lg5)(1＋lg5)＋1－2lg5＋lg²5=2．

16．1．注意在定义域求值．

(三)解答题

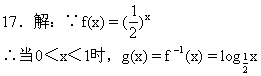
当－1＜x＜0，0＜－x＜1

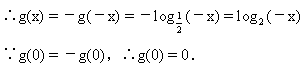
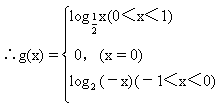
18．证：设任取两个值x₁、x₂∈R且x₁＜x₂

∵f(x₁)－f(x₂)=a(x₁³－x₂³)

=a(x₁－x₂)(x₁²＋x₁x₂＋x₂²)

(1)当a＞0时，f(x₁)＞f(x₂)，函数y在R上是增函数．

(2)当a=0时，函数y为常数函数．

(3)当a＜0时，f(x₁)＞f(x₂)，函数y在R上是减函数．

19．(1)解：f(x)是R上的奇函数，∴f(0)=0．</PGN0213B.TXT/PGN>

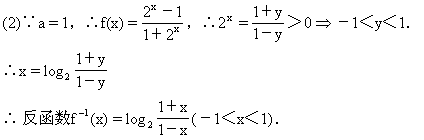
∴定义域为{x－1＜x＜1}

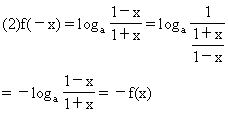
∴f(x)是奇函数

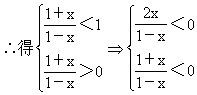
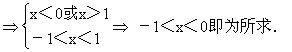
∴(2^P)²－2·2^P－24=0

那么P=log₂6，即均衡价格P₀=log₂6

(2)因为利润=销售额－成本

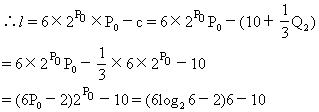
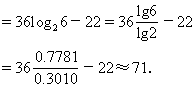
答：利润l的最大值为71．