2000年山师附中高一期中考试数学试卷（11月）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分，考试时间120分钟。
注意事项：
1、答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型（A或B）用铅笔涂写在答题卡上。
2、每小题选出答案后，用铅笔把答题卡上对应题目的答案号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，答案不能答在试卷上。
3、在同一题号中，标有“（实）”的题目由使用实验教材的学生完成，没作标记的由使用普通教材的学生完成。其余题目所有学生都做。
第一卷（选择题，共30分）
一、选择题（本大题共10个小题，每小题3分共30分，在每小题给出的四个选项中，只有一个是符合题目要求的。）
1、（实）若a>b,且ab≠0,则下列结论正确的是（ ）
(A)ac>bc (B)a2>b2 (C)a-c>b-c (D)
（普）下列函数中与函数y=x表示同一函数的是（ ）
（A）
(B)
(C)
(D)
2、已知集合M={m∈Zm=2k+1,k∈Z}与P={p∈Zp=4t±1,t∈Z},则（ ）
(A)
(B) 
(C)
(D)
3、不等式1-2x<3的解集是（ ）
（A）{x∈R-2<x<-1} (B){x∈R-1<x<2}
(C){x∈Rx<2} (D){x∈Rx<-1或x>2}
4、下列命题中为真命题的是（ ）
(A)若x2=1，则x=1. (B)不等式x2>1的解集是{x∈Rx>±1}
(C)若
(D)若
5、已知p和q是两个命题，则p或q为真是p且q为真的（ ）
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
6、(实)已知
（ ）
(A)a>b>c (B)c>b>a (C)b>a>c (D)c>a>b
（普）(x,y)在映射f下的象是
,则在f下(-5,2)的原象是（ ）
(A)(-10,4) (B)(-3,-7) (C)(-6,-4) (D)
7、“若x,y∈R且x2+y2=0,则x,y全为0”的否命题是（ ）
(A)若x,y∈R且x2+y2≠0,则x,y全不为0
(B)若x,y∈R且x2+y2≠0,则x,y不全为0
(C)若x,y∈R且x,y全为0,则x2+y2=0
(D)若x,y∈R且xy≠0,则x2+y2≠0
8、已知集合M={(x,y)x+y=2},N={(x,y)x-y=4},那么集合M∩N为（ ）
(A)x=3,y=-1 (B)(3,-1 (C){3，-1} (D){(3,-1)}
9、(实)已知a,b∈(0,1),则在a2+b2,a+b,2ab,
中最大的一个是（ ）
(A) a2+b2 (B) a+b (C) 2ab (D)
（普）如果奇函数y=f(x)在区间[3,7]上是增函数，且最小值为5，那么y=f(x)在区间[-7,-3]上是（ ）
(A)增函数且最小值为-5 (B)增函数且最大值为-5
(C)减函数且最小值为-5 (D)减函数且最大值为-5
10、(实)
的解集是（ ）
(A)
(B)
(C)
(D)
（普）化简式子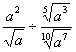
等于（ ）
(A)
(B)
(C)
(D)
11、(实)一个教室的面积为a m2,其窗子的面积为b m2,(a>b),如果
称为这个教室的亮度，现在教室和窗子同时增加c m2,则其亮度（ ）
(A)不变 (B)减小 (C)增加 (D)不确定
（普）已知函数f(x)=x5+px3+qx-8满足f(-2)=10,则f(2)=（ ）
(A)10 (B)-10 (C)-26 (D)-18
12、(实)甲、乙两人同时到同一商店分两次购买面粉，甲每次购买10千克，乙每次购买10元钱的，已知两次价格不同，设甲两次的平均价格为p，乙两次的平均价格为 q,则（ ）
(A)p>q (B)p=q (C)p<q (D)与价格有关
（普）已知不等式x-1+x+a<5的解集非空，则a的取值范围是（ ）
(A)(-4,6) (B)(-6,4) (C)(-∞,-4)∪(6,+ ∞) (D) (-∞,-6)∪(4,+ ∞)
第二卷（共72分）
二、填空题（本大题共5个题，每小题4分，共20分，请将答案写在题中横线上）
13、(实)不等式
的解集是
。
（普）函数
的反函数是
。
14、全集u={x∈Nx≤5},A={1,3},B={3,4,5},那么A∪( uB)= 。
15、把命题 “负数的平方是正数”改写成“若p则q的”的形式为 ；
其逆否命题为 。
16、函数
的定义域为R，则实数k的取值范围是
。
17、(实)已知a<1,b<1,则a+b+a-b 2.(填“>”或“<”)
（普）若
，则x的取值范围是
。
三、解答题（本大题共5个小题，共48分，解答应写出文字说明、证明过程或推理步骤）
18、（本题10分）
写出集合{1，2，3，4，}的所有子集，并指出寻些是它的真子集。
19、（本题12分）
（实）解下列不等式
（1）
（2）
> x+1
(普)判断函数
上的增减性，并加以证明。
20、(本题10分)
（实）已知a,b,c为△ABC的三边,求证:
>0
（普）求函数
的反函数，并画出它的图象。
21、（本题10分）
已知A={xx-1≥a},B={xx2+2x-24<0}且A∩B=φ,求a的范围。
22、（本题10分）
(实)某单位决定投资3200元建一仓库（长方体状），高度2为米，它的后墙用旧墙不花钱，正面用铁栅，每平方米造价20元，两侧墙砌砖，每平方米造价22·5元，顶部每平方米造价20元。试计算：
(1)仓库底面积S的最大允许值是多少？
(2)为使S达到最大，而实际投资又不超过预算，那么正面铁栅应设计为多长？
（普）若奇函数f(x)在定义域(-1,1)上是减函数，求满足f(1-a)+f(1-a2)<0的实数a的取值范围。
期中试题数学答案
选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C | C | B | D | B | B | B | D | B | C | C | A |
实验题第12题为（A）其余与普通题答案相同。
填空题
13．{xx＞3}（实） 
（普）
14．{0，1，2，3}
15．若一个数为负数，则这个数的平方是正数
若一个数的平方不是正数，则这个数不是负数
16．
17．＜（实） -2＜x＜1（普）
18．φ，{1}，{2}，{3}，{4}，{1，2}，{1，3}，{1，4}，{2，3}，{3，4}，{2，4}，
{1，2，3}，{1，2，4}，{1，3，4}，{2，3，4}，{1，2，3，4}
除{1，2，3，4}外都是真子集
19．（实）（1）
∴{xx＜-4或-1≤x＜3或3＜x≤4}
（2）
讨论1：x≥1时，
∴x＞1是原不等式的解
讨论2：x＜1时，
（1）x≥0时，
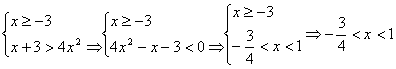
（2）x＜0时，x≥-3
∴-3≤x＜1是原不等式的解
∴原不等式解为{x-3≤x＜1或x＞1}
（普）f（x）在[-∞，-1）上是增函数
证明：任取（-∞，-1）上两实数
，
，设
（∵
，
∴
∴
∴f（x）在（-∞，-1）上是增函数
20．（实）∵
∴
（∵cosC＞-1）
∴
（普）
（x＜-1）
∵x＜-1
∴
改写：
原函数值域{yy＞-1}
∴反函数
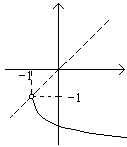
21．A：
或x≤1-a
B：-6＜x＜4
∵A∩B=φ
∴1+a≥4且
∴{aa≥7}
22．（实）
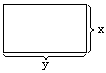
2x·45+40·y+20·xy=3200 S=xy
∵
∴
∴
此时 90x=40y
y=15或y=-24（舍）
∴y=15
（普）-1＜1-a＜1 ① 且
②
③
解：①、②、③取交集得{a0-a<1}