高 一 数 学 练 习 (一)　　　　　　　　　　 

2002.10.　　　　　 班级：_______________；姓名：_________________；成绩：________________

一. 选择题：将下列各题的答案填入表中(每小题3分，共3×8 = 24分)

1. 设A, B, C为三个集合，命题甲：AB且AC；命题乙：A Í (BC)，则甲是乙成立的
　　　(A)充分不必要条件　(B)必要不充分条件　(C)充要条件　(D)即不充分也不必要条件

2. 已知集合M = {(x, y)x + y = 0, x, yÎR}, N = {(x, y) x² + y² = 0, x,yÎR}，则有
　　　(A) MN = M　(B) MN = N　(C) MN = M　(D) MN = Æ

3. 满足条件M{1} = {1, 2, 3}的集合M的个数是
　　　(A) 4　　(B) 3　　 (C) 2　　 (D) 1

4. 设全集U = {a, b, c, d, e}，集合M = {c, d, e}, N = {a, b, e}，那么集合{a, b}可以表示为
　　　(A) MN　　(B) C_UMN　　(C) C_UNM　　(D) C_UMC_­UN

5. 不等式(1 + x)(1－ x ) > 0的解集是　
　　　(A) {x 0 < x < 1} (B) {x x < 0且x ¹－1} (C) {x －1< x < 1} (D) {x x < 1且x ¹－1}

6. 若A = {x x－1 < 2 } , B = {x > 0 } ,则 AB =

　　　(A) {x －1<x<3 }　(B) {x x<0或x>2 }　(C) {x －1<x<0 }　(D) {x －1<x<0或2<x<3}

7. 若不等式ax² + abx + b > 0的解集为{ x 2 < x < 3 } ,则a + b的值为

　　　(A) 5　 (B) 　 (C) －　 (D) 　

8. 下列命题p：x + y > 1且xy > 1；q：x > 1且y > 1，则p是q成立的
　　　(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件

二. 填空题：(每小题4分，共3×8 = 32分)

9. 若AB且AC，B={0,1,2,3,4}，C={0,2,4,8}，则满足上述条件的集合A有________个.

10. 已知全集U = { x x8, xN* }，集合A, B Í U. 如果A(C_UB) = {1 ,8 }, (C_UA)B = {2 ,6 }, (C_uA)(C_uB) ={4,7}，则集合A=_____________________; B = __________________________.

11. 已知集合M = {y y=x²－4x + 3,xR},N = {y y =－x² + 2x + 8,xR},则MN=______________.

12. 用描述法表示以y轴为中心线的宽为1的长带子内(包括边界)的点集_______________________ .

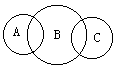
13. 用阴影表示下列集合：[(C_UA)∪(C_UC)]B（如图）　　　　　　　 

14. 已知实数x满足4x²－4x－15 < 0, 化简－x－3　　　 U =___________ .

15. 已知集合A =　{x x² + 3x－18 > 0}, B = {x (x－k)(x－k－1) < 0}，且AB ¹ Æ，则k的取值范围为_______________________ .

16. 不等式0的解集是__________________________ .

三. 解答题：(共44分)

17. 解不等式：x²－3x > 4

18. 解不等式： 3－x + 2x + 1 < 6　　

19. 设a ¹ b，解关于x的不等式：a²x + b²(1－x) > [ax + b(1－x)]².

20. 已知函数y = x²－2kx + 2在x >－1时恒有y > k成立，求实数k的取值范围.

21. 已知实数a > b, 全集U = R, 集合A = {x x²＋(a－1)x－a > 0}, B = {x (x + a)(x + b) > 0 }, M = {x x²－2x－3 < 0}. (1)若C_UB Í M, 求a, b的取值范围；(2)若－1 < b < a < 1,求A∩B；(3)若－3 < a <－1,且a²－1(C_UA)，求实数a 取值范围.

参考答案：

一.

题号	1	2	3	4	5	6	7	8
答案	A	A	C	B	D	D	C	B

二. 9. 8; 　

10. A= {1 ,3 ,5 ,8 },B={2 ,3 ,5 ,6 };

11. [-1,9];

12. {(x,y) -1/2£x£1/2且yÎR};

13. 即为B;

14.1;

15. k< -6 or k > 2;

16. (-3/2,0)È[1,+¥];

三.17. x<-1orx>4;

　18. -4/3 < x < 2;

19. 不等式整理为：(a - b)²(x² - x) < 0∴0 < x < 1; 20. 提示：令F (x) = x²－2kx + 2－k, 则要使在x > -1时f (x) > k恒成立，即使F (x) > 0恒成立∴D_x < 0 或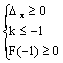, 解得kÎ[-3,1]; 21. 提示：(1)集合M = {x -1 < x < 3}, ∵a > b∴集合B = {x x < -a或x > -b}∴C_UB = {x -a < x < -b}由C_UB Í M，得-1<-a<-b<3 ∴-3 < b < a < 1; (2)∵-1 < b < a < 1∴A={xx< -a or x>1}, B = {x x< -a or x>-b}, AÇB=A; (3) ∵-3 < a < -1且a²－1ÎC_UA∴1 < - a < 3, A = {x x < 1或x > - a}∴1 < a²-1 < - a, ∴aÎ[-1-Ö5/2, -Ö2]