高一数学竞赛试题

姓名：　　　　 　班级：　　　　 得分：　　　　

一、选择题（本大题共15小题，每小题　分，共　 分）

题号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
答案

1、设全集U={2，3，a²+2a-3}，A={a+1，2}，C_UA={5}，则a的值为（　 ）

　　 A、2　　　 B、-3或1　　 C、-4　　  D、-4或2

2、已知函数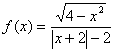，则它是（　　）

A．奇函数　　　　　　　　　　 B．既是奇函数又是偶函数

C．偶函数　　　　　　　　　　 D．既不是奇函数又不是偶函数

3、设x=，则x³-3x²-3x+2=(　　 )

A、0 　　　　　　B、1 　　　　　　C、2　　　　　D、3

4、设A={1，2}，则从A到A的映射中满足f[f(x)]=f(x)的个数是（　　）

A、1个　　　　　 B、2个　　　　　 C、3个　　　 D、4个

5、方程的实根个数（　 ）

A、0　　　　　　　 B、1　　　　　　 C、2　　　　 D、至少两个

6．若关于ｘ的方程ｋ＋＝0有实数解，且ｘ属于第三象限，则ｋ的取值范围是（　　）．

Ａ．ｋ＜　　　　　 Ｂ．ｋ≥－（）　　

Ｃ．＜ｋ＜　　　  Ｄ．ｋ＞（）

7、设函数y=f(x)对于一切实数x都满足f(3+x)=f(3-x), 且方程f(x)=0恰有6个不同的实

根，则这6个根之和为（　　）

A．18　　　　　  B、12　　　　　　  C、9　　　　 D、0

8、对于任意实数x，设函数是2-x²和x中较小者，那么f(x)的最大值为（　 ）

A． - 2　　　　　 B、-1　　　　　　  C、1　　　　 D、2

9、设函数f（x）的定义域为R⁺，且对于任何正实数x、y都有f（xy）=f（x）+f（y），

若f（8）=6，则f（）=（　　 ）

　　　　A、1；　　 B、2；　　 C、－1；　　 D、

10、设有三个函数，第一个函数y=f（x），第二个函数是第一个函数的反函数，第三个函数

的图象与第二个函数的图象关于直线x+y=0对称，那么第三个函数是：（　　 ）

　　　　 A、y=－f（x）；　B、y= ；　C、y=　　Ｄ、ｙ＝

11、已知a－b=3,那么a³－b³－9ab的值是（　　）　

A、3　　 　B、　9　 　　　C、 27　　　  D、81

12、若函数的图象关于直线对称,则可能的值为（　 ）

A、-3　　　　B、-1　　　 　 C、 1　　　　D、 2

13、已知函数的图象关于原点对称,当时,那么当时函数的解析式为（　　）

　 　 A、 　　　　 B、 　　　

C、 　　　　 D、

14、在中，下列几个命题：（1） （2）（3）成等差数列（4）中的对边成等差数列　中正确命题的序号为（　　）

A 、 1　　　　  B、  2　　　　　 C 、3　　　　　　 D 、4

15、对于任意实数,下列不等式中恒成立的是（　 ）

　 　 A、　　 B、　

　　　C、 　　　　　　 D、

二、填空题（本大题共4小题，每小题　分，共　 分）

1、数列，>0，则=　　　　　　  。

2、数列，=2, ,则　　　　　　　　　 。

3、钟表现在是10时整，那么在　　　时，　　 分　　　秒时，分针与时针首次出现重合。

4、已知函数f(x)=x²+px+q，，，若A={2}，

则B=　　　　　　　　　 。

5、若g(x)=1-2x,f[g(x)]=则f(1/2)=___________________

三、解答题（本大题共1大题，共　 分）

中国青年报2001年3月19日报道：中国移动通信将于3月21日开始在所属18个省、市移动通信公司陆续推出“全球通”移动电话资费“套餐”，这个“套餐”的最大特点是针对不同用户采取不同的收费方法。具体方案如下：

方案代号	基本月租（元）	免费时间（分钟）	超过免费时间的话费（元/分钟）
1	30	48	0.60
2	98	170	0.60
3	168	330	0.50
4	268	600	0.45
5	388	1000	0.40
6	568	1700	0.35
7	788	2588	0.30

原计费方案的基本月租为50元，每通话一分钟付0.40元，请问

  1）“套餐”中的第4种收费方式的月话费预约通话量（约通话量是指一个月内每次通话用时之和，每次通话是以分为单位取整计算，如莫茨通话时间为3分20秒，按4分钟即通话时间）的函数关系式；

 2) 取第4种收费方式，通话量多少时原收费方式的月通话费省钱；

 3）据中国以东2000年公布的中期业绩，每户通话连平均为每月320分钟，若一个用户的通话量恰好是这个平均值，那么选择哪种收费方式更合算，并说明理由。