2005学年第二学期萧山六、八、九三校高一期中考试
数 学 试 题 卷
一、选择题:(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项符合题目要求,把答案填在下表中)
1.已知A={第一象限角},B={锐角},C={小于90°的角},那么A、B、C关系是( )
A.B=A∩C
B.B∪C=C C.A![]() C D.A=B=C
C D.A=B=C
2.将分针拨慢5分钟,则分钟转过的弧度数是 ( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
3.已知![]() 的值为 ( )
的值为 ( )
A.-2 B.2 C.![]() D.-
D.-![]()
4. 已知角![]() 的余弦线是单位长度的有向线段;那么角
的余弦线是单位长度的有向线段;那么角![]() 的终边
( )
的终边
( )
A.在![]() 轴上 B.在直线
轴上 B.在直线![]() 上
上
C.在![]() 轴上 D.在直线
轴上 D.在直线![]() 或
或![]() 上
上
5.若![]() ,则
,则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
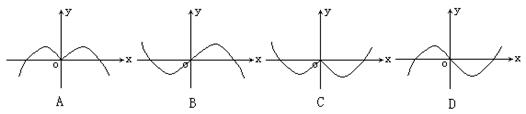 |
6.函数y=-x sinx的部分图像是 ( )
7.下列函数中同时具有①最小正周期是π;②图象关于点(![]() ,0)对称这两个性质的是( )
,0)对称这两个性质的是( )
A.
y=cos(2x+![]() ) B.y=sin(2x+
) B.y=sin(2x+![]() )C.y=sin(
)C.y=sin(![]() +
+![]() )D.y=tan(x+
)D.y=tan(x+![]() )
)
8.已知![]() 的图象和直线y=1围成一个封闭的平面图形,该图形的面积
的图象和直线y=1围成一个封闭的平面图形,该图形的面积
是 ( )
A.4π B.2π C.8 D.4
9.与正弦曲线![]() 关于直线
关于直线![]() 对称的曲线是( )
对称的曲线是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10. 已知![]() ,-
,-![]() <
<![]() <0,则
<0,则![]() 等于 ( )
等于 ( )
A.π-arcsin(-![]() ) B.π+arcsin(-
) B.π+arcsin(-![]() ) C.arcsin(-
) C.arcsin(-![]() ) D.-arcsin(-
) D.-arcsin(-![]() )
)
11.已知函数![]() 在同一周期内,
在同一周期内,![]() 时取得最大值
时取得最大值![]() ,
,![]() 时取得最小值-
时取得最小值-![]() ,则该函数解析式为 (
)
,则该函数解析式为 (
)
A.![]() B.
B.![]()
C![]() D.
D.![]()
12..函数![]() 的图象的相邻两支截直线
的图象的相邻两支截直线![]() 所得线段长为
所得线段长为![]() ,则
,则![]() 的值是
( )
的值是
( )
A.0 B.1 C.-1 D.![]()
二、填空题:(本大题共4小题,每小题4分,共16分。把答案填在题中横线上)
13.已知![]() 的取值范围是
.
的取值范围是
.
14.![]() .
.
15.已知![]() 则
则![]() .
.
16.设函数![]() ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线![]() 对称; ②它的图象关于点
对称; ②它的图象关于点![]() 对称;
对称;
③它的周期是![]() ;
④在区间
;
④在区间![]() 上是增函数。
上是增函数。
以其中两个论断作为条件,余下论断作为结论,写出一个你认为正确的命题:
___________________________________.(用序号表示)
三、解答题:(本大题有5小题,共48分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分7分) 求值![]()
18. (本小题满分7分)已知![]() ,求
,求![]() 的值
的值
19.(本小题满分10分)试求函数y=sinx+cosx+2sinxcosx+2(![]() )的最大值和最小值(12分)
)的最大值和最小值(12分)
20.(本小题满分12分)
某港口的水深![]() (米)是时间
(米)是时间![]() (
(![]() ,单位:小时)函数,下面是该港口的
,单位:小时)函数,下面是该港口的
水深表:
|
| 0 | … | 3 | … | 9 | … | 15 | … |
|
| 10 | … | 13 | … | 7 | … | 13 | … |
|
|
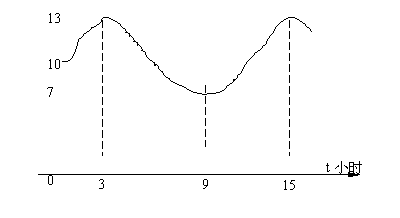 |
经过拟合,该曲线可近似地看成正弦函数![]() (其中A.>0,ω>0)的图象。
(其中A.>0,ω>0)的图象。
(1)试根据数据表和曲线,求函数![]() (其中A.>0,ω>0)的表达式;
(其中A.>0,ω>0)的表达式;
(2)一般情况下,船舶航行时船底同海底的距离不小于4.5米时是安全的,如果某船的吃水深度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,它在港内停留的时间最多不能超过多长时间?(忽略离港所用的时间)
21. (本小题满分12分)已知函数![]() 是R上的偶函数,其图象关于点
是R上的偶函数,其图象关于点![]() 对称,且在区间
对称,且在区间![]() 上是单调函数.求
上是单调函数.求![]() 的值.
的值.
2005学年第二学期六、八、九三校高一期中考试
数学答案
一、选择题: (每小题3分)
a) B 2. C 3. D 4. A 5. A 6.C
7. A 8. B 9 D 10.C 11.B 12.A
二、填空题: (每小题4分)
13.![]()
14.![]()
15.![]()
16.①③![]() ②④ ( 或②③
②④ ( 或②③![]() ①④)
①④)
三、解答题:
17.(本小题满分7分)解:原式![]()
![]()
18.(本小题满分7分)解:![]()
![]()
原式=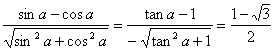
19.(本小题满分10分)解:![]()
![]()
![]() 由二次函数图象性质得
由二次函数图象性质得![]()
20.(本小题满分12分)解:(1)设函数![]()
由图象得![]()
![]()
(2)由题意得
![]() (
(![]() )
)
解得 ![]()
所以船在1时至5时或13时至17时进港是安全的。
它在港内停留时间不得超过16小时。
22.(本小题满分12分)解:由f(x)是偶函数,得f(-x)= f(-x).
即: ![]() 所以-
所以-![]()
对任意x都成立,且![]() 所以得
所以得![]() =0.依题设0
=0.依题设0![]() ,所以解得
,所以解得![]() .
.
由f(x)的图象关于点M对称,得![]() .取x=0,得
.取x=0,得![]() =-
=-![]() ,所以
,所以![]() =0.
=0.

