2005学年源清中学高一数学月考试卷
一、选择题(本大题共10小题,每小题3分,共30分)
1. 设集合P={1,2,3,4,5,6},Q={xÎR2£x£6},那么下列结论正确的是
A.P∩Q=P B.P∩Q![]() Q C.P∪Q=Q D.P∩Q
Q C.P∪Q=Q D.P∩Q![]() P
P
2. 函数y=![]() 的定义域是
的定义域是
A.(1,2] B.(1,2) C.(2,+¥) D.(–¥,2)
3. 设函数y=f(x)存在反函数是y=f –1(x),若f(a)=b,则f –1(b)是
A.a B.a–1 C.b D.b–1
4. 函数f(x)=2x2–mx+3,当xÎ[–2,+¥)时是增函数,当xÎ(–¥,–2]时是减函数,则f(1)等于
A.–3 B.13 C.7 D.由m而定的常数
5. 不等式组![]() 的解集是{xx>2},则实数a的取值范围是
的解集是{xx>2},则实数a的取值范围是
A.a£–6 B.a³–6 C.a£6 D.a³6
6. 若3x–1<3,化简![]() +
+![]() 的结果是
的结果是
A.6x–2 B.–6 C.6 D.2–6x
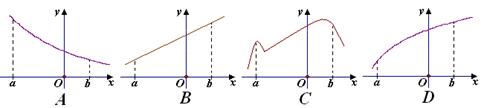
7. 对于任意x1、x2Î[a,b],满足条件f(![]() )>
)>![]() [f(x1)+f(x2)]的函数f(x)的图象是
[f(x1)+f(x2)]的函数f(x)的图象是
8. 若定义在区间(–1,0)上的函数f(x)=log2a(x+1)满足f(x)>0,则a的取值范围是
A.(0,![]() ) B.(0,
) B.(0,![]() ] C.(
] C.(![]() ,+∞) D.(0,+∞)
,+∞) D.(0,+∞)
9. 已知命题p:“一次函数的图象是一条直线”,命题q:“函数y=ax2+bx+c(a、b、c为常数)的图象是一条抛物线”.则下列四种形式的复合命题中真命题是
①非p ②非q ③p或q ④p且q
A.①② B.①③ C.②③ D.③④
10. 若数列{an}的前n项和Sn=n2–2n+3,则数列{an}的前3项依次为
A.–1,1,3 B. 6,1,3 C. 2,1,3 D.2,3,6
二、填空题(本大题共5小题,每小题4分,共20分)
11. 设T={(x,y)ax+y–3=0},S={(x,y)x–y–b=0}.若S∩T={(2,1)},则a×b =________.
12. 等比数列的公比为2,前5项和为1,则其前10项和为_______.
13. 1992年底世界人口达到54.8亿,若人口的年平均增长率为1%,经过x年后世界人口数为 y亿,则y与x的函数解析式为_________.
14. 已知a、b是两个命题,如果a是b的充分条件,那么![]() a是
a是![]() b的_______条件.
b的_______条件.
(填“充分条件”、或“必要条件”、或“充要条件”)
15. 若函数y=ax与y= –![]() 在(0,+∞)上都是减函数,则函数y=ax2+bx在(0,+∞)上是单调递_______函数.(填“增函数”或“减函数”)
在(0,+∞)上都是减函数,则函数y=ax2+bx在(0,+∞)上是单调递_______函数.(填“增函数”或“减函数”)
三、解答题(本大题共5小题,每小题10分,共50分.解答应写出文字说明、证明过程或演算步骤)
16. 已知U=R,A={xx–2>1},B={x![]() ³0},求A∩B,A∪B,(∁UA)∪B.
³0},求A∩B,A∪B,(∁UA)∪B.
17. 已知在逐项递增的等差数列{an}中,a1+a4+a7=15,a2×a4×a6=45,求其通项an.
18. 已知函数![]() .
.
(Ⅰ)画出函数的简图;(Ⅱ)求该函数的值域(仅由图象指出其值域得2分).
19. 某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆. 本年度为适应市场需求,计划提高产品档次,适当增加投入成本. 若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应的提高比例为0.75x,同时预计年销售量增加的比例为0.6x.
(Ⅰ)写出本年度预计的年利润y与投入增加的比例x的关系式;
(Ⅱ)为使本年度的年利润比上年有所增加,问投入成本增加的比例x应在什么范围内.
20. 已知f(x)=log4(2x+3–x2).
(Ⅰ)求f(x)定义域;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)求f(x)的最大值,并求取最大值时x的值.
四、附加题(本大题共2小题,每小题10分,共20分)
21. 已知a<0,设p:实数x满足x2–4ax+3a2<0;q:实数x满足x2–x–6£0或x2+2x–8>0. 若![]() p是
p是![]() q的必要不充分条件,求a的取值范围.
q的必要不充分条件,求a的取值范围.
22. 若关于x的方程4x+(a+3)×2x+5=0至少有一个实根在区间[1,2]内,求实数a的取值范围.
2005学年源清中学高一数学月考试卷答卷
一、选择题(本大题共10小题,每小题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题(本大题共5小题,每小题4分,共20分)
11._________;12.______________;13.________________;14.__________;15.____________
三、解答题(本大题共5小题,每小题10分,共50分)
16. 已知U=R,A={xx–2>1},B={x![]() ³0},求A∩B,A∪B,(∁UA)∪B.
³0},求A∩B,A∪B,(∁UA)∪B.
17. 已知在逐项递增的等差数列{an}中,a1+a4+a7=15,a2×a4×a6=45,求其通项an.
18. 已知函数![]() .
.
 (Ⅰ)画出函数的简图;
(Ⅰ)画出函数的简图;
(Ⅱ)求该函数的值域(仅由图象指出其值域得2分).
19. 某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆. 本年度为适应市场需求,计划提高产品档次,适当增加投入成本. 若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应的提高比例为0.75x,同时预计年销售量增加的比例为0.6x.
(Ⅰ)写出本年度预计的年利润y与投入增加的比例x的关系式;
(Ⅱ)为使本年度的年利润比上年有所增加,问投入成本增加的比例x应在什么范围内.
20. 已知f(x)=log4(2x+3–x2).
(Ⅰ)求f(x)定义域;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)求f(x)的最大值,并求取最大值时x的值.
四、附加题(本大题共2小题,每小题10分,共20分)
21. 已知a<0,设p:实数x满足x2–4ax+3a2<0;q:实数x满足x2–x–6£0或x2+2x–8>0. 若![]() p是
p是![]() q的必要不充分条件,求a的取值范围.
q的必要不充分条件,求a的取值范围.
22. 若关于x的方程4x+(a+3)×2x+5=0至少有一个实根在区间[1,2]内,求实数a的取值范围.
参考答案:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | A | B | B | C | D | A | C | C |
11. 1 12. 33 13. y=54.8´1.01x 14. 必要条件 15. 减函数
16. A∩B={xx<1或x>3},A∪B={xx£1或x>2},(∁UA)∪B=R
17.an=2n–3
18.(0,1]
19.(1)y=–60x2+20x+200
(2)0<x<![]()
20.(1)(–1,3)
(2) f(x)的减区间是(1,3),增区间是(–1,1)
(3)当x=1时,f(x)取最大值1.
21.a£–4或![]() £a<0
£a<0
22.![]()
