扬州大学附属中学
高一数学练习（十一月）
班级＿＿＿＿ 姓名＿＿＿＿ 学号＿＿＿＿ 成绩＿＿＿＿
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1． 倾斜角为135°，在
轴上的截距为
的直线方程是（ ）
A．
B．
C．
D．
2． 原点在直线l上的射影是P(－2，1)，则直线l的方程是 （ ）
A．
B．
C．
D．
3． 如果直线
是平面
的斜线，那么在平面内(
)
A．不存在与平行的直线
B．不存在与垂直的直线
C．与垂直的直线只有一条 D．与平行的直线有无穷多条
4． 过空间一点作平面，使其同时与两条异面直线平行，这样的平面（ ）
A．只有一个 B．至多有两个
C．不一定有 D．有无数个
5． 直线
与直线
关于原点对称，则
的值是 (
)
A．
=1，
= 9
B．=－1，= 9
C．=1，=－9
D．=－1，=－9
6． 已知直线
上两点P、Q的横坐标分别为
，则PQ为 （ ）
A．
B．
C．
D．
7． 直线
通过点(1，3)且与两坐标轴的正半轴所围成的三角形面积为6，则直线的方程是 （ ）
A．
B．
C．
D．
8． 如果一个正三棱锥的底面边长为6，则棱长为
，那么这个三棱锥的体积是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
9． 一平面截一球得到直径是6cm的圆面，球心到这个平面的距离是4cm，则该球的体积是 ( )
A．
B．
C．
D．
10． 
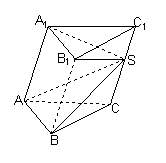在体积为15的斜三棱柱ABC－A1B1C1中，S是C1C上的一点，S－ABC的体积为3，则三棱锥S－A1B1C1的体积为 （ ）
A．1
B．
C．2 D．3
11． 已知点
、
直线过点
，且与线段AB相交，则直线的斜率的取值
范围是 （ ）
A．
或
B．或
C．
D．
12． 过点（1，2），且与原点距离最大的直线方程是（ ）
A．
B．
C．
D．
二、填空题：
13． 过点
且在两坐标轴上截距相等的直线的方程是＿＿＿＿＿＿＿＿＿＿＿＿．
14． 过点(－6，4)，且与直线
垂直的直线方程是＿＿＿＿＿＿＿＿＿＿＿．
15． 
在正方体ABCD—A1B1C1D1中，BC1与平面BB1D1D所成的角是
．
16． 已知两点
，
，直线
与线段AB相交，则
的取值范围是
．
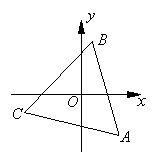
17． 如图，△ABC为正三角形，且直线BC的倾斜角是45°，则直线AB，，AC的倾斜角分别为：
__________， 
____________．
18． 正四面体（所有面都是等边三角形的三棱锥）相邻两侧面所成二面角的余弦值是 ．
三、解答题：
19． 已知平行四边形的两条边所在的直线方程分别是x＋y＋1＝0和3x－y＋4＝0， 它的对角线的交点是M(3， 0)， 求这个四边形的其它两边所在的直线方程．
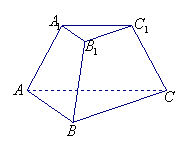
20． 正三棱台的上、下底边长为3和6．
（Ⅰ）若侧面与底面所成的角是60°,求此三棱台的体积；
（Ⅱ）若侧棱与底面所成的角是60°,求此三棱台的侧面积；
21． 在△ABC中，BC边上的高所在的直线的方程为
，∠A的平分线所在直线的方程为
，若点B的坐标为（1，2），求点 A和点 C的坐标．．
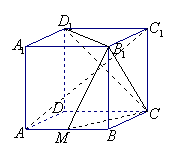
22． 如图，在正方体ABCD—A1B1C1D1中，已知M为棱AB的中点．
（Ⅰ）AC1//平面B1MC；
（Ⅱ）求证：平面D1B1C⊥平面B1MC．
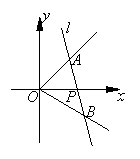
23． 如图，射线
、
分别与
轴成
角和
角，过点
作直线
分别与、交于
、
．
（Ⅰ）当的中点为
时，求直线的方程；
（Ⅱ）当的中点在直线
上时，求直线的方程．
