高一数学期中考试试卷
一．填空题(每小题4分，共40分)：
1． 已知集合
，集合
，则
＿＿＿。
2． 设全集
，集合
，则
＿＿＿＿＿＿。
3．“
”是“
”的＿＿＿＿＿＿＿条件。
4．不等式组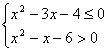
的解集为＿＿＿＿＿＿＿（用区间表示）。
5．已知函数
，则函数
的值域为＿＿＿＿＿＿＿＿。
6．已知偶函数
当
时，
，则当
时，函数的表达式为＿＿＿＿＿＿＿＿。
7．不等式
的解集为＿＿＿＿＿＿＿＿＿＿＿＿。
8．已知函数
在
上单调递减，则实数
的取值范围是＿＿＿＿＿＿＿＿＿＿。
9．试写出命题：“若
是一元二次方程
的两个根，则
且
”的一个等价命题：＿＿＿＿＿＿＿＿＿＿＿＿＿
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。
10．若二次函数
和
满足
是R上的减函数，试给出一组满足条件的二次函数
。
二．选择题(每小题3分，共12分，每题只有一个正确的答案)：
11．全集
，对于数集
，若
，则下列集合表示空集的是（ ）
A．
B．
C． D．
12．下列不等式一定成立的是 （ ）
A．
B．
C．
D．
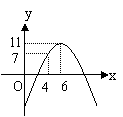13．某汽车公司购买了一批豪华大客车投入营运，据分析每辆客车营运的总利润y（万元）与客车营运的年数
之间的关系为二次函数（如图），则每辆客车营运多少年，其年平均利润最大。 （ ）
A．3年 B．4年 C．5年 D．6年
14．已知偶函数的定义域为R，它在
上单调递减，设
，则
的大小关系为 （ ）
A．
B．
C．
D．
三．解答题(本大题满分48分，解答本题应写出必要的过程)：
15．(本题满分8分)
已知集合
，若 
，求实数的范围。
16．(本题满分10分)
设
，函数
是R上的奇函数
(1)求实数的值； (2)判断并证明函数在R上的单调性。
17．(本题满分10分)
已知二次函数
在区间
上的最大值为9，求实数
的值。
18．(本题满分10分)
已知边长为1的正方形ABCD（如图），P是对角线BD上的点，连结AP延长AP交BC或其延长线于Q，设DP= x，y为△ADP和△BPQ的面积之和。
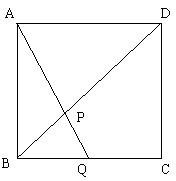(1)写出y关于x的函数关系式；
(2)当x为何值时，y有最小值，并求出最小值。
19．(本题满分10分)
设是定义在R上的奇函数，对于任意的
，当
时，都有
。
(1)试证明函数在R上单调递增；
(2)解不等式
高一数学期中考试试卷(参考答案)
一．填空题(每小题4分，共40分)：
3． 已知集合，集合，则
。
4． 设全集，集合，则
。
3．“”是“”的 充分非必要 条件。
4．不等式组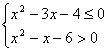的解集为
（用区间表示）。
5．已知函数，则函数的值域为
。
6．已知偶函数当时，，则当时，函数的表达式为 
。
7．不等式的解集为
。
8．已知函数在上单调递减，则实数的取值范围是
。
9．试写出命题：“若是一元二次方程的两个根，则且”的一个等价命题：“若
或
，则不全是一元二次方程的根”。
10．若二次函数和满足是R上的减函数，试给出一组满足条件的二次函数
。
二．选择题(每小题3分，共12分，每题只有一个正确的答案)：
11．全集，对于数集 ，若，则下列集合表示空集的是（A）
A． B． C． D．
12．下列不等式一定成立的是 （C）
A． B．
C． D．
13．某汽车公司购买了一批豪华大客车投入营运，据分析每辆客车营运的总利润y（万元）与客车营运的年数之间的关系为二次函数（如图），则每辆客车营运多少年，其年平均利润最大。 （C）
A．3年 B．4年 C．5年 D．6年
14．已知偶函数的定义域为R，它在上单调递减，设
，则的大小关系为 （D）
A．
B． C． D．
三．解答题(本大题满分48分，解答本题应写出必要的过程)：
15．(本题满分8分)
已知集合，若
，求实数的范围。
解：
：
又
∴ 
16．(本题满分10分)
设，函数是R上的奇函数
(1)求实数的值； (2)判断并证明函数在R上的单调性。
解：(1) ∵ 是R上的奇函数
∴ 
∴ 
(2)设
则：
所以函数在R上单调递增。
17．(本题满分10分)
已知二次函数函数在区间上的最大值为9，求实数的值。
解：∵ 
(1)当
时：
当
时，
(2)当
时：
当
时，
所求的实数的值为
。
18．(本题满分10分)
已知边长为1的正方形ABCD（如图），P是对角线BD上的点，连结AP延长AP交BC或其延长线于Q，设DP= x，y为△ADP和△BPQ的面积之和。
(1)写出y关于x的函数关系式；
(2)当x为何值时，y有最小值，并求出最小值。
解：(1) ∵ 
，∴ 
又 
∽
∴ 
则：
(2) 
∴当且仅当
时，
19．(本题满分10分)
设是定义在R上的奇函数，对于任意的，当时，都有
(1)试证明函数在R上单调递增；
(2)解不等式
解：(1) 设则：
所以函数在R上单调递增。
(2) 
又函数在R上单调递增
