辽宁省实验中学2000—2001学年度下学期期中阶段测试

高一年级数学试卷

　　本试卷参考公式：

　　　　　　

　　　　　　

　　　　　　

　　　　　

　　第I卷　（选择题　共60分）

　　一、选择题：（本大题共12小题，每题5分，共60分。在每题所给出的四个选项中，只有一个是正确的）

　　1．的值等于

　　A．　　　　　B．　　　　C．　　　　D．

　　2．集合，，则

　　A．M=N　　　　B．　　　　C．　　　　D．M∩N=φ

　　3．要得到函数的图象，只要将函数y=sin2x的图象

　　A．向左平行移动个单位　　　　B．向右平行移动个单位

　　C．向左平行移动个单位　　　　D．向右平行移动个单位

　　4．函数y=f(x)的图象上每个点的纵坐标保持不变，将横坐标伸长到原来的2倍，然后再将整个图象沿x轴向左平行移动个单位得到的图象，则y=f(x)的表达式是

　　A．　　　　　　B．

　　C．　　　　　　D．

　　5．已知△ABC中，tanAtanB>1，那么△ABC

　　A．一定是锐角三角形　　　　 B．一定是直角三角形

　　C．一定是钝角三角形　　　　 D．形状不确定

　　6．的值等于

　　A．　　　　B．　　　　C．　　　 D．

　　7．函数f(x)=cos2x-sinx+1（）的最大值为M，最小值为m，则

　　A．M=2，m=1　　　　　  B．，m=1

　　C．M=2，m=-1　　　　　 D．，m=-1

　　8．已知且cosα+cosβ>0，则下列式子成立的是

　　A．α+β<π　　　　 B．

　　C．　　　　D．

　　9．已知tanα、tanβ是方程的两个根，且，则α+β等于

　　A．　　　　　　　 B．

　　C．　　　　D．

　　10．函数的最小正周期是

　　A．　　　　 B．　　　　　 C．π　　　 D．2π

　　11．α、β、γ均为锐角，若，则α、β、γ的大小关系是

　　A．α<β<γ　　　 B．α<γ<β

　　C．γ< β<α　　  D．β<γ<α

　　12．已知奇函数f(x)在[-1，0]上为单调递减函数，又α、β为锐角三角形两内角，则

　　A．f(cosα)>f(cosβ)　　　　 B．f(sinα)>f(sinβ)

　　C．f(sinα)>f(cos)β　　　　 D．f(sinα)<f(cosβ)

　　第II卷　（非选择题　 共90分）

　　二、填空题：（本大题共4个小题，每小题4分，总计16分。请把你认为正确的答案填在横线上）

　　13．设α、β均为锐角，，，则cosβ=_________________。

　　14．_________________。

　　15．给出下列命题：

　　①存在实数x，使得sinxcosx=1成立；

　　②存在实数x，使成立；

　　③函数是偶函数；

　　④方程是函数的图象的一条对称轴方程；

　　⑤若α、β是第一象限角，且α>β，则tanα>tanβ。

　　其中正确命题的序号是_________________。

　　16．设，且，则_________________。

　　三、解答题：（本大题共6题，总计74分。解答请写出文字说明、计算步骤和证明过程）

　　17．（本题10分）

　　已知，求的值。

　　

　　18．（本题12分）

　　已知f(x)=asinx+bcosx

　　（1）当，且f(x)的最大值为时，求a、b的值。

　　（2）当，且f(x)的最小值为k时，求k的取值范围。

　　

　　19．（本题12分）

　　求的值。

　　

　　20．（本题12分）

　　已知，且，，求sin（α+β）的值。

　　

　　21．（本题14分）

　　求函数的最大值，并求出取得最大值时x的集合。

　　

　　22．（本题14分）

　　已知函数f(x)=asinx+acosx+1-a（a∈R），。若定义在非零实数集上的奇函数g(x)在（0，+∞）上是增函数，且g(2)=0，求当g[f(x)]<0时实数a的取值范围。

　　

　　辽宁省实验中学2000—2001学年度下学期期中阶段测试

　　高一年级数学试卷答案及评分标准

　　一、选择题：

　　1．A　 2．C　 3．D　4．C　5．A　 6．D　 7．B　 8．D　 9．D　 10．C　 11．B　 12．D

　　二、填空题：

　　13．　　 14．4　　 15．③④　　 16．

　　三、解答题：

　　17．解：原式样　　 2分

　　　　　　　　　　　　　　　　　　　  6分

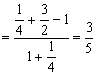　　　　　　　　　　　　　　　　　　　　　 10分

　　18．解：（1）由得a+b=2 ①　　又由f(x)的最大值为得　②

　　解① ②得a=3，b=-1或a=-1，b=3　　　　　　　　　  5分

　　（2）由得　　③　 ⑥又　　④

　　知k<0，且有　 ⑤　　 将③代入⑤得　　 8分

　　整理得：　⑥　因为a∈R　 故△≥0，得

　　所以k<0　　所以k≤-1　　　　　　　　　　　  12分

　　19．解：原式

　　　　　　  6分

　　　　　　　　　　　　　　　　　　　　　　　　　10分

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

　　20．解：因为，

　　所以，　　 2分

　　又因为，

　　所以，　　  6分

　　所以　　8分

　　　　　　　　　　  10分

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 　　　　　12分

　　21．解：原式　　4分

　　

　　　　　　 　　　6分

　　　　　　　　　　　　 8分

　　所以 当时，f(x)取得最大值　 10分

　　这时即　　  12分

　　22．解：

　　根据已知条件　由g(x)<0可得x∈（-∞，-2） Y（0，2）　　2分

　　由题意，要g[f(x)]<0，即要f(x) ∈（-∞，-2）或f(x)∈（0，2）恒成立

　　若 恒成立，则

　　因为，所以，当x=0或时，不满足，

　　所以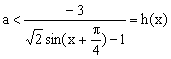而h(x)无最小值，故这时的a不存在。　 6分

　　若　恒成立，

　　则

　　当x=0或时，a∈R；　　　8分

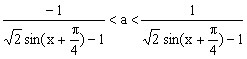　　当时，则恒成立

　　所以，　　　　　　 12分

　　综上，当x=0或时，a∈R；当时，　14分