济南市高一数学试题（2001、1）

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷至1至2页，第Ⅱ卷2至8页，满分120分，测试时间120分钟。

第Ⅰ卷（选择题共50分）

注意事项：

1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型用铅笔涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上。（如无答题卡，请将正确选项的代号填在题后括号内）。

一、选择题：本大题共15小题。第（1）—（10）题每小题3分；第（11）—（15）小题每小题4分；共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．不等式4x-3＜21的解集是（　　）

（A）{x＜x＜6}　　 （B）{xx＜}

（C）{xx＞6}　　　　　  （D）{xx＞6或x＜}

2．如集合A满足{1，2}则集合A的个数为（　 ）

（A）1（B）2（C）3（D）4

3．命题：在△ABC中，如果∠C=90°，那么，则该命题的四种形式中，是真命题的共有（　　）

（A）1个（B）2个（C）3个（D）4个

4．已知数列中，=1，，则等于（　 ）

（A）（B）（C）（D）

5．U={1,2,3,4,5},A={2,3},B={3,4,5}则下列计算中的一个是（　 ）
（A）[={1,4,5}　　 （B）[={1,2}

（C）A∪B={2,3,4,5}　　（D）A∩[={1,2,3}

6．在命题①“a＞b＞0”是“＞”的充分条件；②“a＞b＞0”是“＞”的必要条件；③“a＞b”是“a＞b”的充要条件；④“a＞b”是“a+c＞b+c”的充要条件；其中真命题是（　）

（A）①②　　　　（B）②③　　　　（C）①④　　　　（D）③④

7．等比数列中，=625，则等于（　 ）

（A）25（B）±5（C）5（D）±25

8．已知函数=ƒ(x)是奇函数, =g(x)是偶函数,且g(x)ƒ(x)≠0,则下面结论中的是（　　）

（A）ƒ(x)+ g(x)是偶函数　 （B）(x)+(x)是偶函数

（C）g(x)·ƒ(x)是奇函数　　（D）是奇函数

9．某居委会对其管辖区300户居民生活水平进行调查，统计结果为：有电冰箱270户，有VCD音响248户，二者都有的233户，则电冰箱和VCD至少有一种的户占总户数的百分数为（　 ）

（A）80%（B）95%（C）98%（D）100%

10．当x=10，y=-27时，的值为（　　）

（A）-3（B）-30（C）（D）-60

11．已知U=R，且A={x-16＜0}，B={x-4x+3≥0}，则下列求解结果正确的是（　 ）

（A）A∩B={x-4＜x≤1}　　 （B）A∪B={x3＜x＜4}

（C）(A∩B)={xx≤-4或1＜x＜3或x＞4}　 （D）（A）∩（B）≠Ø

12．已知函数y=x+b与y=ax+8互为反函数，在ƒ(x)=a+bx中，ƒ(0)，ƒ(1)，ƒ(3)之间的大小关系为（　 ）

（A）ƒ(0) ＜ƒ(1) ＜ƒ(3)　 （B）ƒ(1)＜ƒ(3)＜ƒ(0)

（C）ƒ(3)＜ƒ(1) ＜ƒ(0)　　　（D）ƒ(1) ＜ƒ(0)＜ƒ(3)

13．已知A、B两地相距150km，某人开汽车以60km/h的速度从A地到达B地，在B地停留一小时后再以50km/h的速度返回A地，把汽车离开A地的距离x表示为时间t的函数，函数表达式为（　　）

（A）x=60t　　 （B）x=

（C）x=60t+50t　（D）x=

14．如数列的前n项和满足，则（　 ）

（A）可能是等比数列（B）可能是等差数列

（C）一定是等比数列（D）一定是等差数列

15．y= ƒ(x)是奇函数，当x＜0时，ƒ(x)=x(1-x)，则当x＞0时，(x)应等于（　　）

（A）-x (x+1) (x＞0)　　　（B）（x＞0）

（C）（x＞0）　（D）x (1+x) (x＞0)

第Ⅱ卷（非选择题共70分）

二、填空题：本大题共5小题。每小题3分，共15分。将答案填在题中横线上。

16．函数ƒ(x)=的定义域是_____________________________ 。

17．用适当的集合填空

∪	Ø　　　　　　 A　　　　　　 A
Ø A A	____________　 ____________　　____________ ____________　 ____________　  ____________ ____________　 ____________　　____________

18．已知(x+y)=3, (x-y)=－2,则=__________________。

19．设集合A={a,a+d,a+2d}, B={a,aq,a},如A=B,则q=______________________。

20．定义在区间（－∞，+∞）的奇函数ƒ(x)为增函数；偶函数g(x)在〔0，+∞）的图象与ƒ(x)的图象重合，设a＞b＞0，给出下列不等式；

①ƒ(b)- ƒ(-a)＞g(a)-g(-b);　②ƒ(b)- ƒ(-a)＜g(a)-g(-b);

③ƒ(a)- ƒ(-b)＞g(b)-g(-a);　④ƒ(a)- ƒ(-b)＜g(b)-g(-a).

其中成立的是_______________________ （写上序号即可）

三、解答题：本大题共6小题。共55分。解答要写出文字说明、证明过程或解题步骤。

21．（本小题满分8分）

画出下列函数的图象（不列表，直接在坐标系中画出即可）。

（1）ƒ(x)=3x+1　 x∈N　且x≤3；

（2）y=（0＜a＜1）。

22．（本小题满分8分）

（1）在等差数列中，已知=7，=16。求公差d和的值；

（2）在等比数列中，已知，q=－3，=81。

求：n和的值。

23．（本小题满分9分）

（1）求函数反函数(x)；

（2）解不等式组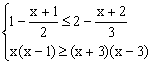

24．（本小题满分10分）

函数ƒ(x)=，其定义域为x∈〔-a,1-a〕,如此函数有最大值25,求取得最大值时x的值.

25．（本小题满分10分）

某企业2000年年初投入资金1000万元，预计每年的资金增长率为50%，每年年底扣除成本（工人工资、奖金、原料消耗等）外，其余资金全部投入到下一年，如2003年年初的投入资金达到2000万元，则每年的成本应控制在多少万元内？（精确到万元）

26．（本小题满分10分）

已知函数ƒ(x)=。

（1）求ƒ(x)的定义域；

（2）判断ƒ(x)的单调性并用定义加以证明；

（3）当x为何值时ƒ〔x(x-)＜.

参考答案

一、1.A　2.B  3.D　4.C　5.D  6.C　7.B　8.A  9.B　10.D　11.D　12.D　13.D　14.B　15.C

二、16.{xx≠-2}　17.略（3个空1分）　18. 15　 19.　20.①③

三、21．（1）坐标系正确2分，图正确2分

（2）坐标系正确1分，标出（0，1）点1分，图象做出2分。

22．（1）方法一：②-① 得d=3……………………………………3分

=1，∴=1+4×3=13…………………………………………………………………4分

方法二：∴d=3………………………………………………3分

同理=13…………………………………………………………………………………4分

（2）81=（-3）即=-27∴n-1=-3　n=4…………………………………6分

……………………………………………………………………8分

23．（1）由（x≠0）得(y-1)=y+1…………………………………………1分

x=……………………………………………………………………3分

∴y=……………………………………………………5分

（2）原式化为…………………………………………………7分

…………………………………………………………………9分

24．此抛物线开口向下，对称轴为x=………………………………………………1分

当∈〔-a,1-a〕即时…………………………………………………………2分

最大值应为ƒ()=4+3=25

得内取不到最大值.………………………………………4分

当＞1-a即a＞时，ƒ(x)在[-a,1-a]上递减

∴ƒ(-a)=25得a=

∴x=-a=……………………………………………………………………………………9分

综上，当x=-或x=时ƒ(x)有最大值25………………………………………………10分

25．解：设控制在x万元内…………………………………………………………………1分

则第一年扣除成本投入下一年资金为

1000×(1+50%)―x=1000×―x…………………………………………………………3分

第二年扣除成本投入下一年资金为

(1000×―x) (1+50%)―x=1000×―(1+)x………………………………………5分

第三年扣除成本后结余

1000×―[1++]x=2000…………………………………………………………7分

解得 x=289万元…………………………………………………………………9分

答：应控制在289万元之内…………………………………………………………………10分

26．（1）由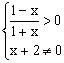得ƒ(x)的定义域是（-1，1）………………………………………2分

（2）ƒ(x)在（-1，1）上是减函数…………………………………………………………3分

设则

ƒ()-ƒ()=

=……………………………………………………4分

∵∴　

∴

∴……………………………………………6分

∴ƒ()-ƒ()＜0　∴ƒ()＜ƒ()

∴ƒ(x)在（-1，1）上是减函数………………………………………………………………7分

（3）∵ƒ(0)=

∴ƒ[x(x)]＜ƒ(0)由函数的单调性有

0＜x(x)＜1

∴…………………………………………………………10分