高一学年下学期期中考试题（数学）

班级：_____________　姓名：_____________　考号：_____________

一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项符合题目要求的，请将所选答案涂在答题卡上。

1．Sin600°

A．　　　 B．　　　 C．　　　 D．

2．下列四组角：（1）　　（2）　 （3）　　（4）

（k∈Z）终边相同的是

A．（1），（2）　　　　B．（1），（2），（3）

C．（1），（2），（4）　 D．（1），（2），（3），（4）

3．若α为第一象限角，那么sin2α，cosα，，，中必定取正值的有

A．0个　　　 B．1个　　　 C．2个　　　 D．3个

4．在三角形ABC中，已知sinAsinB<cosAcosB，则三角形ABC的形状为

A．锐角三角形　　 B．直角三角形　　 C．钝角三角形　　 D．形状不确定

5．设θ∈（0，2π），若sinθ<0，且cos2θ<0，则θ的范围是

A．　　 B．　　　C．　　 D．

6．函数的周期T=4π，那么常数ω为

A．　　　　B．2　　　 C．　　　 D．4

7．若函数f(x)=cos2x+8sinx，则它的最大，最小值分别是

A．最大值是9，最小值是-9

B．最大值是9，最小值是7

C．最大值是7，最小值是-9

D．最大值是7，最小值不存在

8．函数的图象是轴对称图形，则它的一条对称轴可以是

A．y轴　　　B．直线　　  C．直线　　  D．直线

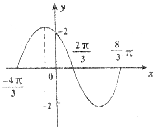
9．函数在一个周期的图象如图所示，求函数解析式

A．　　　 B．

C．　　　 D．

10．将y=sin2x的图象向左平移，得到的曲线对应的解析式为

A．　　　　 B．

C．　　　　D．

11．求函数的定义域

A．　　  B．

C．　　　 D．

12．直角坐标系中，，是单位圆上的两点，则角的余弦值应是

A．　　  B．　　 C．　　 D．

二、填空题：本大题共4小题，每小题4分，共16分，请将答案填在第二页指定的位置上。

13．已知扇形的面积是，半径是1，则扇形的圆心角是_____________。

14．函数的值域是__________________________。

15．化简：__________________________。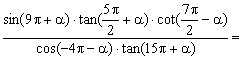

16．若y=a+bsinx的值域是，则此函数的表达式是_____________。

三、解答题（本大题6小题，共74分，解答应写出文字说明，证明过程或演算步骤）

17．已知，，且α∈（0，π），，求β的值。（12分）

18．已知，且，求sinθ和cosθ的值。（12分）

19．已知

（1）用五点法画出它的一个周期的闭区间上的简图。

（2）指出这个函数的周期，振幅，初相。

（3）指出这个函数的单调区间。（12分）

20．已知函数，且，求值域。（12分）

21．已知f(x)是定义在R上的奇函数，且当x>0时，f(x)=sinx+cosx，求f(x)在R上的解析式。（12分）

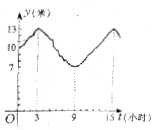
22．某港口的水深y（米）是时间t（0≤t≤24，单位：小时）的函数，下面是该港口的水深表：

t（小题）	0	…	3	…	9	…	15	…
y（米）	10	…	13	…	7	…	13	…

经过长时间的观察，描出的曲线如图所示，经拟合，该曲线可近似的看成正弦函数y=Asinωt+B的图象。

（1）试根据数据表和曲线，

求出函数y=Asinωt+B的表达式；（其中A>0，w>0）

（2）一般情况下，船舶航行时船底同海底的距离不少于4.5米时是安全的。如果某船的吃水深度（船底与水面的距离）为7米，那么该船在什么时间段能够安全进港？若该船欲当天安全离港，它在港内停留的时间最多不能超过多长时间（忽略离港所用的时间）？

参考答案：

一、选择题，本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的，请将所选答案涂在答题卡上。

1．D　　2．D　　3．C　　4．C　　5．B　　6．C　　7．C　 8．B　　9．C　　10．C

11．B　 12．A

二、填空题：本大题共4小题，每小题4分，共16分，请将答案填在第二页指定的位置上。

13．

14．

15．+1

16．

三、解答题（本大题6小题，共74分，解答应写出文字说明，证明过程或演算步骤）

17．解：∵α∈（0，π），

∴又

∵　　

 ∴

∵　 α∈（0，π）

∴　　∴

∵

∴（α+β）-α∈（0，π）

即　β∈（0，π）

∵β∈（0，π）

∴

18．解：∵

∴sinθ>cosθ>0　　sinθ+cosθ>0

∵　　 sinθ-cosθ>0

∴

　（1）

∴　 （2）

（1）+（2）得

（1）-（2）得

19．解：

（1）

x
	0		π		2π
	0	3	0	-3	0

（2）T=4π　　A=3　　

（3）为递减区间

为递增区间

20．解：

∵　　∴ -π≤2x≤0　　

　　 

∴值域为[-7，-1]

21．解：设x<0　 则-x>0　 ∵x>0时f(x)=sinx+cosx

∴f(-x)=sin(-x)cos(-x)=-sinx+cosx

∵f(x)为奇函数　 ∴f(x)=-f(-x)=-(-sinx+cosx)=sinx-cosx

因f(x)是定义在R上的奇函数　∴f(0)=0

综上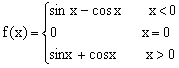

22．解：（1）A=13-10=3

T=15-3=12　　　　B=10

则

（2）y-7≥4.5　　 即y≥11.5

　

（k∈Z）

12k+1≤t=17k+5（k∈Z）

∵0≤t≤24

∴k=0或k=2

当k=0时，1≤t≤5

当=1时，12≤t≤17

故当1时至5时或12时至17时，时间段能够安全进港，该船当天安全离港，它在港内停泊的时间最多不能超过17-1=16（小时）