E1-071　n（＞3）名乒乓球选手单打比赛若干场后，任意两个选手已赛过的对手恰好都不完全相同，试证明，总可以从中去掉一名选手，而使在余下的选手中，任意两个选手已赛过的对手仍然都不完全相同．

【题说】  1987年全国联赛二试题3．

【证】　用英文字母表示选手，用M_A表示A的对手集，并假定A是赛过场次最多（若有并列的可任选一名）的选手．若命题不成立，则存在B、C，使得去掉A后B、C的对手集相同．由于M_B≠M_C，所以A恰与B、C中一个赛过，不妨设B∈M_A、C M_A．

同样存在D、E，D∈M_C、E M_C，去掉C后，D、E的对手集相同．因为A M_C，所以D不是A；又D∈M_C，所以D∈M_B，即B∈M_D=M_E∪{C}，从而B∈M_E．C M_E，而去掉A后，B、C的对手集相同，因此E=A．

于是M_A=M_E=M_D\{C}，即M_A比M_D少一个元素C，与A为赛过场次最多的假设矛盾．命题得证．

E1-072　一个俱乐部中有3n+1个人，每两个人可以玩网球、象棋或乒乓球，如果每个人都有n个人与他打网球，n个人与他下棋，n个人与他打乒乓球，证明俱乐部中有3个人，他们之间玩的游戏是三种俱全．

【题说】  1987年匈牙利数学奥林匹克题3．

【证】　将人看作平面上的点，得到一个有3n+1个点的图（假定任意三点都不在一直线上），当两个人玩网球或象棋或乒乓球时，我们就在相应的两点之间连一条红线或黄线或蓝线，需要证明的是，一定存在一个三条边的颜色互不相同的三角形．

自一点引出的3n条线段中，如果某两条线段的颜色不同，就称它们构成一个“异色角”．考虑异色角的个数．由于自每一点引出n条红线，

角形中有3个异色角．这个三角形的三条边颜色互不相同，即相应的三个人之间玩的游戏是三种俱全．

E1-073  在一块平地上有n个人，对每个人，他到其他人的距离均不相同，每人都有一把水枪，当发出火警信号时，每人用枪击中距他最近的人，当n为奇数时，证明至少有一个人身上是干的．当n为偶数时，此结论是否正确？

【题说】　第十九届（1987年）加拿大数学奥林匹克题4．

【证】　设n=2m-1，对m进行归纳，

m=1，结论显然正确．

假设n=2k-1时结论正确，对于2k+1个人，其中距离最近的两人设为A、B．剩下的2k-1人中，依归纳假设，有一个人C身上是干的．因AC＞AB，BC＞AB．故把A、B考虑进去时，C身上仍是干的．

若n是偶数，则结论不成立．例如n=2m个人站成两排，同排两两相距均大于1米，前后两人相距1米．那么当火警信号发出后，前后两人互射，谁也免不了挨水枪．

E1-075　在第一行中写有19个不超过88的自然数，第二行写有88个不超过19的自然数，我们将一行中的一个或数个相连的数称为一段．证明：可以从上述两行数中各选出一段来，使得这两段数的和相等．

【题说】　第二十二届（1988年）全苏数学奥林匹克八年级题4．

【证】　设a₁，a₂，…，a₁₉为第一行数；b₁，b₂，…，b₈₈是第二行数．

记　　　　　　　　　　　　　　　　　　  A（i）=a₁+…+a_i

B（i）=b₁+…+b_i

假定　　　　　　　　　　　　　　　　　　　　 A（19）≥B（88）

（对于A（19）＜B（88）的情形可类似处理）对于每个i，记

n_i=min{n；A（n）≥B（i），1≤n≤19}

根据假设，这样的n_i是存在的．我们来考察88个差数A（n_i）-B（i）．显然它们的值为整数，且都在0至87之间，这是因为

如果这88个差数互不相同，则它们之中必有一个为0，于是我们的命题获证．

否则，这88个差数中至少有某两个相等，不妨设

i₁=l，i₂=k，l＜k

使得

A（n_l）-B（l）=A（n_k）-B（k）

于是就有

A（n_l）-A（n_k）=B（l）-B（k）

显然，题意中的19、88可以换成任意自然数．

E1-076  将8×8方格纸板的一角剪去一个2×2正方形，问余下的60个方格能否剪成15块形如 的小纸片？

【题说】　第四届（1989年）东北三省数学邀请赛二试题3．

【解】　如图a，在余下的60个方格中填上1与-1，从左到右每列正负相间．显然任一块剪下的纸片中，四个数的和为2或-2．

若能剪成15块，设其中和为2的有x块，和为一2的有y块，则

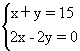
这方程组的唯一解x=y=15／2不是整数，这就表明不可能剪成15块所述形状的纸片．

【别解】　若将小方格如图b填上1和-1，则任一块剪下的纸片中数字之和为1或-1．于是15块数字总和不为0，但整个图b数字之和为0．矛盾．

E1-077  有五只猴子和五个梯子．每个梯子的顶端各放一根香蕉．梯子之间有若干绳子相连．每条绳子连接两个梯子，任一梯子的同一级上没有两条绳子，开始时五只猴子位于不同梯子底端．它们沿梯子向上爬，遇到绳子就沿它爬到另一端，然后继续上爬．求证：无论有多少绳子，最后每只猴子都各拿到一根香蕉．

【题说】　第二十一届（1989年）加拿大数学奥林匹克题4．

【证】　甲数学归纳法．当绳子根数为0时，结论显然成立．设有n根绳子，其中一根绳子连结第一个梯子的A与第二个梯子的B，而A以下不再有绳子．我们将第一个梯子从A、第二个梯子从B锯下来，并将第一个梯子下段接于第二梯子上段，作为第一个梯子；第二个梯子下段接于第一个梯子上段，作为第二个梯子．这样便归结于（n-1）根绳子的情况．

E1-078　某地区网球俱乐部的20名成员举行14场单打比赛，每人至少上场一次．求证：必有6场比赛，其12个参赛者各不相同．

【题说】　第十八届（1989年）美国数学奥林匹克题2．

【证】　作一个图G：20个顶点A₁，…A₂₀，表示20个选手，14条边表示14场比赛，顶点A_i的次数（由它出发的边数）为d_i（i=1，2，…，20）．则

从顶点A_i抹去（d_i-1）条边（同一条边可以同时被其二端点抹去），最多抹去

条边，所余子图G′中至少还有6条边，而各顶点度皆≤1．这表明至少有6场比赛的参赛者各不相同．

E1-079  100个运动员参加赛跑，已知其中任意12个人中总有两个彼此熟悉的，证明：运动员的号码不论如何编排（未必是从1到100），总可以找到两个彼此熟悉的运动员，他们的号码是以相同的数字开头的（即最高数位的数字相同）．

【题说】　第十六届（1990年第三阶段）全俄数学奥林匹克十年级题7．

【解】　用N_i（i=1，2，…，9）表示以数字i开头的号码的数目．只须证明：对于某个k，有N_k≥12即可．事实上，若对所有的i=1，

题得证．

E1-080  一条马路上有六个车站（如图），今有一辆汽车由a₁驶向a₆，沿途各站可自由上下乘客，但此辆汽车在任何时候至多可载乘客5人，试证：在此六站中必有两对（四个不同的）车站A₁、B₁；A₂、B2，使得没有乘客在A₁站上而且在B₁站下（A₁在B₁之前），也没有乘客在A₂站上而且在B₂站下（A₂在B₂之前）．

【题说】  1957年北京市赛高三二试题8．

【证】　设在站a_i（i=1，2，3）上车、站a_j（j=4，5，6）下车的人数为b_ij．在车从a₃开往a₄的途中，这些人全在车上．由于车上至多载客5人，b_ij（i=1，2，3；j=4，5，6）中至少有4个为0．其中有两个具有相同的i，不失一般性，可以假定b₁₄=b₁₅=0．在b_2j，b_3j（j=4，5，6）中至少有一个为0．不妨设b₂₄=0，则站a₁，a₅；a₂，a₄即为所求的两对车站．