涡阳四中高一数学上学期期末测试卷
命题人:史学祥 ( 2006。1。10)
一.选择题(每题所给四个选项中有且只有一个选项符合题目要求,请将该选项序号填涂到答题卡上,每题5分,共60分)
1.若![]() ,
,![]() ,则满足
,则满足![]() ,且
,且![]() 的集合C的个数为
的集合C的个数为
A.3个 B.4个 C.7个 D.8个
2.下列四组中的函数![]() 、
、![]() ,表示同一个函数的是
,表示同一个函数的是
A.![]() B.
B.![]()
|
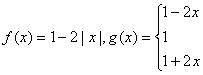
3 “1+![]() >0”是“(x+2(x-1)
>0”的
>0”是“(x+2(x-1)
>0”的
A 充分不必要条件 B 必要不充分条件 C 充要条件 D 既不充分也不必要条件
4.等比数列![]() 各项均为实数,且
各项均为实数,且![]() ,则
,则![]() 等于
等于
A.±2 B.±16 C.±4 D.16
5.在等差数列![]() 中,已知
中,已知![]() ,前n项和为Sn,则Sn的最大值为
,前n项和为Sn,则Sn的最大值为
A.144 B.143 C.121 D.120
6.某企业在今年初贷款a万元,年利率为r,从今年末开始每年来偿还一定金额,预计5年内还清,则每年应偿还的金额为
A.![]() 万元
B.
万元
B.![]() 万元
万元
C.![]() 万元
D.
万元
D.![]() 万元
万元
7 若函数f(x)的图象经过点(-1,0),则函数f-1(x+4)的图象必过点
A (-1,4) B (-4,-1) C(-1,-4) D (1,4)
8.已知全集U = R,集合![]() ,
,![]() ,且CUA
,且CUA![]() ,则a的取值范围是
,则a的取值范围是
A.![]() B.(1,3) C.[ 1,3 ] D.
B.(1,3) C.[ 1,3 ] D.![]()
9.设函数![]() 的反函数是
的反函数是![]() ,则方程
,则方程![]() 的解是
的解是
A.![]() B.
B.![]() C.
C.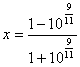 D.
D.![]()
10.已知数列{an}满足![]() 记
记![]() ,则下列结论正确的是
,则下列结论正确的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.已知函数![]() ,构造函数
,构造函数![]() 定义如下,当
定义如下,当![]() 时,
时,
![]() ;当
;当![]()
![]() 时,
时,![]() ,那么
,那么![]()
A.有最小值![]() ,无最大值 B.有最小值0,无最大值
,无最大值 B.有最小值0,无最大值
C.有最大值1,无最小值 D.无最小值,也无最大值
12.函数![]() 的图像如图所示,它在R上为减函数,现有如下结论:
的图像如图所示,它在R上为减函数,现有如下结论:
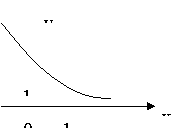
![]() ①
① ![]() ②
② ![]()
|
|
![]() 其中正确结论的个数为
其中正确结论的个数为
A.1 B.2
C.3 D.4
二.填空题(每题4分,共16分,把正确的答案填在题中的“_____”线上。)
13.若函数![]() 在区间
在区间![]() 上单调递减,则a的取值范围是_______________。
上单调递减,则a的取值范围是_______________。
14.不等式![]() 的解集是__________________。
的解集是__________________。
15.已知数列![]() 和
和![]() 都是等差数列,它们的前n项和分别记为Sn和Tn,且
都是等差数列,它们的前n项和分别记为Sn和Tn,且![]() ,则
,则![]() _____________。
_____________。
16.关于函数![]() ,
,![]() 有以下命题:
有以下命题:
①![]() 的值域为实数集R,则
的值域为实数集R,则![]() 或
或![]() ;
;
②![]() 的定义域为实数集R,则
的定义域为实数集R,则![]() ;
;
③![]() 在
在![]() 上为增函数,则
上为增函数,则![]() ;
;
④![]() 为偶函数的充要条件为
为偶函数的充要条件为![]() 。
。
其中正确的命题的序号是_________(把你认为正确的命题的序号都填上)。
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17 (12)已知集合A={x∈R∣![]() <0},B={ x∈R∣x2+ax+b≤0},
<0},B={ x∈R∣x2+ax+b≤0},
A∩B=ф A∪B={ x∈R∣-4<x≤3}, 求实数a、b的值。
18
(12)用单调性定义证明:f(x)=![]() 在(-∞,0)上是增函数
在(-∞,0)上是增函数
19(本题满分12分)
设等差数列![]() 的前n项和为Sn,
的前n项和为Sn,![]() ,数列
,数列![]() 满足
满足![]() 。问是否存在常数k,使数列
。问是否存在常数k,使数列![]() 成等差数列?若存在,求出这样的k值;若不存在,说明理由。
成等差数列?若存在,求出这样的k值;若不存在,说明理由。
20(本题满分12分)
我国是水资源比较贫乏的国家之一许多城市采用价格调控等手段,提醒市民节约用水,某市按月收取用户的水费公式是:
水费 = 基本用水费 + 超额用水费 + 定额损耗费
该市规定:
①若月用水量不超过最低限量m立方米,不管用水多少,都需付基本用水费9元和每户每月的定额损耗费a元;
②若月用水量超过m立方米,除了付基本用水费和定额损耗费外,超过部分每立方米付n元的超额用水费。
③用户每月的定额损耗费不超过4元。
(Ⅰ)请写出用户月水费y(元)与月用水量x(立方米)的函数关系式,并注明函数的定义域。
(Ⅱ)该市一用户今年第一季度每月的用水量和支付费用如下表所示:
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 2.5 | 10 |
| 二 | 3.5 | 14 |
| 三 | 4 | 18 |
请结合上表数值,确定m、n、a的值。
21 (13)已知函数f(x)是定义在(0,∞)的增函数,且f(xy)= f(x)+ f(y)
①
证明:f(![]() )=f(x)- f(y)
)=f(x)- f(y)
② 已知f(3)=1, 且f(a)>f(a-1)+2 ,求a的取值范围。
22.(本题满分14分)
已知一次函数![]() 与二次函数
与二次函数![]()
![]()
(1)求证:函数![]() 的图象有两个不同的交点A,B;
的图象有两个不同的交点A,B;
(2)设A1,B1是A,B两点在x轴上的射影,求线段A1B1长的取值范围;
(3)求证:当![]() 时,
时,![]() 恒成立.
恒成立.