嵊州中学高一新生素质测试

数学试卷

一、填空题：（每题5分，共30分）

1．　　  若、是方程的两个实根，则的值是＿＿＿＿。

2．　　  已知梯形两底角之和为90°，上底长为5，下底长11，则连结两底中点的线段长为＿＿＿＿。

3．　　  2003年10月15日9时9分50秒，我国“神舟”五号载人飞船准确进入预定轨道。16日5时59分，返回舱与推进舱分离，向地面返回。其间飞船绕地球飞行了60万千米。“神舟”五号载人飞船共巡天飞行了＿＿＿＿秒，飞船的平均速度是＿＿＿＿千米/秒（答案取整数）。

4．　　  抛物线在轴上截得的线段长度的最小值等于＿＿＿。

5．　　  下面是按照一定规律画出的一列“树型”图：

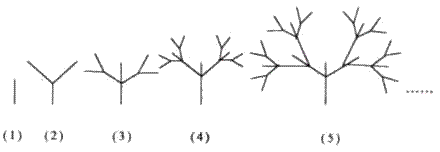
经观察可以发现：图（2）比图（1）多出2个“树枝”，图（3）比图（2）多出5个“树枝”，图（4）比图（3）多出10个“树枝”，照此规律，图（7）比图（6）多出＿＿＿个“树枝”。

6．　　  求值：＿＿＿＿。

二、选择题（每题5分，共30分）

7．小敏用10元钱购买两种邮票：“羊城地铁”每张0.80元，“珠江新桥”每张1.50元，每种至少购1张，多购不限，不同的购买方法种数有（　　　）

A.33　　　B.34　　　C.32　　　D.30

8．已知＝，记的个位数字是x，十位数字是y，则x+y的值是（　　　）

A.3　　　B.7　　　C.13　　　D.15

9．如果对于某一特定范围内的任意允许值，的值恒为一常数，则此值为（　　　）

A.2　　　B.3　　　C.4　　　D.5

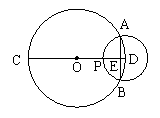10．如图，CD是⊙O的直径，以D为圆心的圆与⊙O交于A与了B两点，AB交CD于点E，CD交⊙D于P，已知PC＝6，PE∶ED＝2∶1，则AB的长为（　　　）

A.　　　B.　　　C.　　　D.

11．化简得（　　　）

A.　　　B. 　　　C. 　　　D.

12．如图，点P是内一点，已知，，那么（　　　）

A.4　　　B.3.5　　　C.3　　　D.无法确定

三、解答题（共40分）

13．（10分）某校开校运会时，某班共有28名同学参加比赛，有15人参加游泳比赛，有8人参加田径比赛，有14人参加球类比赛，同时参加游泳和田径的有3人，同时参加游泳和球类比赛的有3人，没有人同时参加三项比赛，问同时参加田径和球类比赛的有多少人？只参加游泳一项比赛的有多少人？

14．（10分）如图2，△AOB为正三角形，点B坐标为（2,0），过点C（-2，0）作直线L交AO于D，交AB于E，且使△ADE和△DCO的面积相等，求直线L的函数解析式。

表1　各部每1万元营业额所需人数表
部门	百货部	服装部	家电部
人数	5	4	2
表2　各部每1万元营业额所得利润表
部门	百货部	服装部	家电部
利润（万元）	0.3	0.5	0.2

15．（10分）某新建商场设有百货部、服装部和家电部三个经营部，共有190名售货员，计划全商场日营业额为60万元，根据经验，各部商品每1万元营业额所需售货员人数如表1，每1万元营业额所得利润情况如表2。商场将计划日营业额分配给三个经营部，同时适当安排各部的营业员人数，若商场预计每日的总利润为S（万元）且满足19≤S≤20，又已知商场分配给经营部的日营业额均为正整数万元，问这个商场怎样分配日营业额给三个部？各部分别安排多少名售货员？

16．（10分）规定：正整数n的“H运算”是①当n为奇数时，H＝3n+13；②当n为偶数时，H＝n（其中H为奇数）。

如：数3经过1次“H运算”的结果是22，经过2次“H运算”的结果是11，经过3次“H运算”的结果是46。

请解答：（1）数257经过257次“H运算”得到的结果。

　　　　（2）若“H运算”②的结果总是常数a，求a的值。